江苏省无锡市惠山区2020年数学中考二模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 实数4的算术平方根是( )A、±2 B、16 C、2 D、-22. 函数y= 中自变量x的取值范围是( )A、x≠﹣4 B、x≠4 C、x≤﹣4 D、x≤43. 下列运算正确的是( )A、(ab)2=ab2 B、a2·a3=a6 C、(- )2=4 D、×=4. 下列地方银行的标志中,既不是轴对称图形,也不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列说法正确的是( )A、一组数据2,2,3,4,这组数据的中位数是2 B、了解一批灯泡的使用寿命的情况,适合抽样调查 C、小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分 D、某日最高气温是 ,最低气温是 ,则该日气温的极差是6. 如图是由5个大小相同的小正方体组成的几何体,则它的左视图是( )
5. 下列说法正确的是( )A、一组数据2,2,3,4,这组数据的中位数是2 B、了解一批灯泡的使用寿命的情况,适合抽样调查 C、小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分 D、某日最高气温是 ,最低气温是 ,则该日气温的极差是6. 如图是由5个大小相同的小正方体组成的几何体,则它的左视图是( ) A、
A、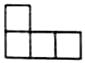 B、
B、 C、
C、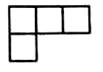 D、
D、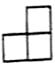 7. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
7. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )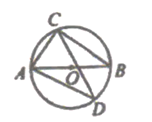 A、35° B、45° C、55° D、65°8. 10个全等的小正方形拼成如图所示的图形,点P、X、Y是小正方形的顶点,Q是边XY一点.若线段PQ恰好将这个图形分成面积相等的两个部分,则 的值为( )
A、35° B、45° C、55° D、65°8. 10个全等的小正方形拼成如图所示的图形,点P、X、Y是小正方形的顶点,Q是边XY一点.若线段PQ恰好将这个图形分成面积相等的两个部分,则 的值为( )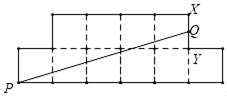 A、 B、 C、 D、9. 如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到 .若反比例函数 的图象恰好经过 的中点D,则k的值是( )
A、 B、 C、 D、9. 如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到 .若反比例函数 的图象恰好经过 的中点D,则k的值是( )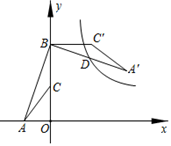 A、9 B、12 C、15 D、1810. 已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )A、﹣1≤t≤0 B、﹣1≤t C、 D、t≤﹣1或t≥0
A、9 B、12 C、15 D、1810. 已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )A、﹣1≤t≤0 B、﹣1≤t C、 D、t≤﹣1或t≥0二、填空题
-
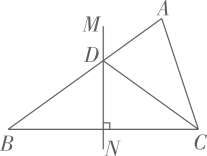
11. 因式分解: .12. 肥皂泡的泡壁厚度大约是 , 用科学记数法表示为 .13. 已知一个多边形的内角和是720°,则这个多边形是 边形.14. 已知圆锥的母线长为5cm,侧面积为15π ,则这个圆锥的底面圆半径为cm.15. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为.
 16. 某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,即整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,则该品牌饮料一箱有瓶.17. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为.
16. 某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,即整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,则该品牌饮料一箱有瓶.17. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为. 18. 如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则 的最大值是.
18. 如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则 的最大值是.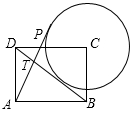
三、解答题
-
19. 计算:(1)、(2)、(2x﹣y)2﹣(x+y)(x﹣y)20.(1)、解方程:x2-6x-6=0;(2)、解不等式组:21. 如图,在▱ABCD中,点E、F分别在边CD、AB上,且满足CE=AF.
 (1)、求证:△ADE≌△CBF;(2)、连接AC,若AC恰好平分∠EAF,试判断四边形AECF为何种特殊的四边形?并说明理由.22. 某校为检测“停课不停学”期间九年级学生的复习情况,进行了中考数学模拟测试并从中随机抽取了部分学生的测试成绩分成 个小组,根据每个小组的人数绘制如图所示的尚不完整的频数分布直方图.
(1)、求证:△ADE≌△CBF;(2)、连接AC,若AC恰好平分∠EAF,试判断四边形AECF为何种特殊的四边形?并说明理由.22. 某校为检测“停课不停学”期间九年级学生的复习情况,进行了中考数学模拟测试并从中随机抽取了部分学生的测试成绩分成 个小组,根据每个小组的人数绘制如图所示的尚不完整的频数分布直方图.
请根据信息回答下列问题:
(1)、若成绩在 分的频率为 ,请计算抽取的学生人数并补全频数分布直方图;(2)、在此次测试中,抽取学生成绩的中位数在分数段中;(3)、若该校九年级共有960名学生,成绩在80分以上的(含80分)为优秀,请通过计算说明,大约有多少名学生在本次测试中数学成绩为优秀.23. 甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.(1)、若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是;
(2)、若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
24. 已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B. (1)、请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)(2)、在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E;(不要求写作法,保留作图痕迹)25. 某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.
(1)、请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)(2)、在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E;(不要求写作法,保留作图痕迹)25. 某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.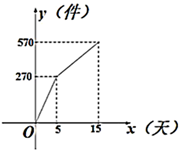 (1)、直接写出y与x的函数关系式;(2)、由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第x天创造的利润为w元,直接利用(1)的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)26. 如图,在△ABC中,AB=BC=10,tan∠ABC= ,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
(1)、直接写出y与x的函数关系式;(2)、由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第x天创造的利润为w元,直接利用(1)的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)26. 如图,在△ABC中,AB=BC=10,tan∠ABC= ,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t. (1)、如图①,当点P在点B,点M是AP中点时,试求AN的长;(2)、如图②,当 = 时,
(1)、如图①,当点P在点B,点M是AP中点时,试求AN的长;(2)、如图②,当 = 时,①求点N到BC边的距离(用含t的代数式表示);
②当点P从点B运动至点C时,试求点N运动路径的长.
27. 已知:在平面直角坐标系xOy中,二次函数y=mx 2 +2mx-4(m≠0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.(1)、求这个二次函数的解析式;(2)、点D的坐标为(-2,1),点P在二次函数的图象上,∠ADP为锐角,且tan∠ADP=2,求出点P的横坐标;28. (操作体验)如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下:

第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于 ;
所以图中 即为所求的点.(1)在图②中,连接 ,说明∠ =30°
(方法迁移)
(1)、如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).(2)、已知矩形ABCD,BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为.(3)、已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为.