江苏省泰州泰兴市、医药高新区2020年数学中考模拟试卷

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣8的立方根是（）

A、﹣2 B、±2 C、2 D、﹣ $\frac{1}{2}$

查看试题解析
2. 如图，四个图标分别是剑桥大学、北京大学、浙江大学和北京理工大学的校徽的重要组成部分，其中是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图是一个正方体展开图，把展开图折叠成正方体后，“抗”字一面相对面上的字是（）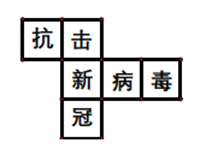

A、新 B、冠 C、病 D、毒

查看试题解析
4. 一元二次方程 $x^{2} - 4 x + 2 = 0$ 根的情况是（）

A、无实数根 B、有两个正根 C、有一个正根，一个负根 D、有两个负根

查看试题解析
5. 下列说法：①事件发生的概率与实验次数有关；②掷10次硬币，结果正面向上出现3次，反面向上出现7次，由此可得正面向上的概率是0.3；③如果事件A发生的概率为 $\frac{5}{100}$ ，那么大量反复做这种实验，事件A平均每100次发生5次.其中正确的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 已知 $m^{2} = 4 n + a$ ， $n^{2} = 4 m + a$ ， $m \neq n$ ，则 $m^{2} + 2 m n + n^{2}$ 的值为（）

A、16 B、12 C、10 D、无法确定

查看试题解析

二、填空题

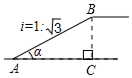
7. 《战狼2》中“犯我中华者，虽远必诛”，令人动容、热血沸腾.其票房突破5600000000元，将5600000000用科学记数法表示为.

查看试题解析
8. 因式分解： $81 - n^{2} =$ .

查看试题解析
9. 若 $x^{2} - 2 y = 1$ ，则 $2 x^{2} - 4 y + 3 =$ .

查看试题解析
10. 如果一个正多边形的内角和等于720°，那么该正多边形的一个外角等于度.

查看试题解析
11. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的坡度i＝1： $\sqrt{3}$ ，则坡角α为度.

查看试题解析
12. 某跳远队甲、乙两名运动员最近 10 次跳远成绩的平均数均为 402 cm，若甲跳远成绩的方差为S_甲2 =66.73，乙跳远成绩的方差为S_乙2 =85.21，则成绩比较稳定的是.（填“甲”或“乙”）

查看试题解析
13. 如图，AB∥CD，DE∥CB，∠B＝m°，则∠D＝°（用含m的代数式表示）.

查看试题解析
14. 如图，⊙O的半径为2，AB是⊙O的切线，A.为切点.若半径OC∥AB，则阴影部分的面积为.

查看试题解析
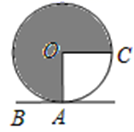15. 如图，在Rt△ABC中，∠ACB＝90°，AC＝6，点G是△ABC的重心，GH⊥BC，垂足是H，则GH的长为.

查看试题解析
16. 图1为一艺术拱门，下部为矩形ABCD，AB、AD的长分别为 $2 \sqrt{3}$ m和4m，上部是圆心为O的劣弧CD，∠COD＝120°.现欲以点B为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2所示.设BC与地面水平线所成的角为 $θ$ ，记拱门上的点到地面的距离为h，当h取最大值时，此时 $θ$ 为°.

查看试题解析

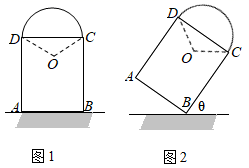
三、解答题

17.

(1)、计算： $\sqrt{\frac{1}{8}} + {(- 2020)}^{0} - \cos 45 °$

(2)、化简： $(\frac{x^{2} - 3}{x - 1} - 2) \div \frac{1}{x - 1}$

查看试题解析
18. 为了解某小区居民使用共享单车次数的情况，某研究小组随机采访该小区的10位居民，得到这10位居民一周内使用共享单车的次数统计如下：

使用次数

0

5

10

15

20

人数

1

1

4

3

1

(1)、这10位居民一周内使用共享单车次数的中位数是次，众数是次.

(2)、若小明同学把数据“20”看成了“30”，那么中位数，众数和平均数中不受影响的是.（填“中位数”，“众数”或“平均数”）

(3)、若该小区有2000名居民，试估计该小区居民一周内使用共享单车的总次数.

查看试题解析
19. 有若干个仅颜色不同的红球和黑球，现往一个不透明的袋子里装进2个红球和2个黑球.

(1)、随机摸出一个球是黑球的概率为；若先从袋子里取出m个红球（不放回），再从袋子里随机摸出一个球，将“摸到黑球”记为事件A.若事件A为必然事件，则m＝；

(2)、若从袋子里一次摸出两个球，用列表法或画树状图法列出所有等可能结果，并求摸出的两球颜色不同的概率.

查看试题解析
20. 在数学课上，老师提出如下问题：
已知：线段AB，求作：∠CAD，使得AB平分∠CAD.

小亮是这样操作的：如图：

①分别以A、B为圆心，大于 $\frac{1}{2}$ AB长为半径画弧，两弧相交于C、D；

②作射线AC、AD，则∠CAD即为所求请根据小亮的作图过程证明AB平分∠CAD.

查看试题解析
21. 新冠肺炎疫情期间，我市对学生进行了“停课不停学”的线上教学活动.某中学为了解这期间九年级学生数学学习的情况，开学后进行了两次诊断性练习.综合成绩由两次练习成绩组成，其中第一次练习成绩占40%，第二次练习成绩占60%.当综合成绩不低于135分时，该生数学学科综合评价为优秀.

(1)、小明同学的两次练习成绩之和为260分，综合成绩为132分，则他这两次练习成绩各得多少分？

(2)、如果小张同学第一次练习成绩为120分，综合成绩要达到优秀，他的第二次练习成绩至少要得多少分？

查看试题解析
22. 如图，点A（2，m），B（－2，3m）分别在反比例函数 $y_{1} = \frac{2}{x} (x > 0)$ 和 $y_{2} = \frac{k}{x} (k < 0 ， x < 0)$ 的图象上，经过点A、B的直线与y轴相交于点C.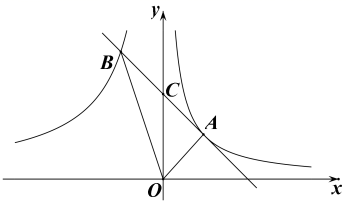

(1)、求m和k的值；

(2)、求△AOB的面积.

查看试题解析
23. 如图，△ABC是⊙O的内接三角形.AE是⊙O的直径，交BC于点G.过点A作AF⊥BC，AF分别与BC、⊙O交于点D、F，连接BE、CF.

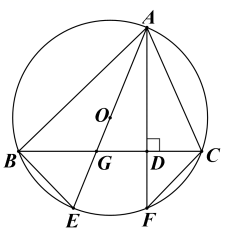(1)、求证：∠BAE＝∠CAF；

(2)、若AB＝8，AC＝6，AG＝5，求AF的长.

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x - 3$ 过A（－1，0）、B（3，0），直线AD交抛物线于点D，点D的横坐标为2，点P（m，n）是线段AD上的动点.

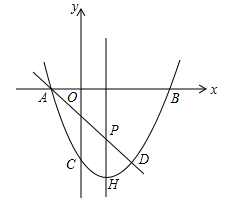(1)、求抛物线和直线AD的解析式；

(2)、过点P的直线垂直于x轴，交抛物线于点H，
①求线段PH的长度l与m的关系式；

②当PH＝2时，求点P的坐标.

查看试题解析
25. 如图1，矩形ABCD中，AD＝2，AB＝a，点E为AD的中点，连接BE.过BE的中点F作FG⊥BE，交射线BC于点G，交边CD于H点.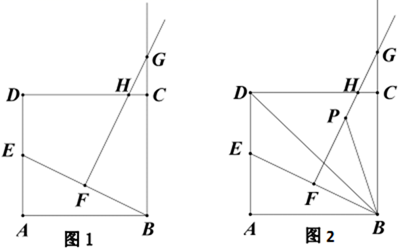

(1)、连接HE、HB
①求证：HE＝HB；

②若a＝4，求CH的长.

(2)、连接EG，△BEG面积为S
①BE＝ ▲ （用含a的代数式表示）；

②求S与a的函数关系式.

(3)、如图2，设FG的中点为P，连接PB、BD.猜想∠GBP与∠DBE的关系，并说明理由.

查看试题解析
26. 如图，在平面直角坐标系中，直线 $y = - x + 6$ 分别与x、y轴交于A、B两点，将直线AB沿着y轴翻折，交x轴负半轴于点C.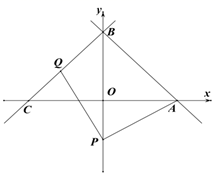

(1)、求直线BC的函数关系式；

(2)、点P（0，t）在y轴负半轴上，Q为线段BC上一动点（不与B、C重合）.连接PA、PQ，PQ＝PA
①若点Q为BC中点，求t的值；

②用t的代数式表示点Q的坐标和直线PQ的函数关系式；

③若M（2m，n－8），N（t³＋2t²－2m，n）在直线PQ上，求n的取值范围.

查看试题解析

使用次数	0	5	10	15	20
人数	1	1	4	3	1