江苏省苏州市张家港市2020年数学中考适应性卷

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 3的相反数是（）

A、-3 B、 $\sqrt{3}$ C、3 D、±3

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算中，正确的是（）

A、 $a^{4} + a^{4} = a^{8}$ B、 $a^{4} • a^{4} = 2 a^{4}$ C、 ${(a^{3})}^{4} \cdot a^{2} = a^{14}$ D、 ${(2 x^{2} y)}^{3} \div 6 x^{3} y^{2} = x^{3} y$

查看试题解析

4. 下表是苏州10个市(区)今年某日最低气温(℃)的统计结果:

县(区)

姑苏区

吴江区

高新区

吴中区

相城区

工业

园区

太仓市

昆山市

常熟市

张家港

气温(℃)

则该日最低气温(℃)的中位数是（）

A、15.5 B、14.5 C、15 D、16

查看试题解析

5. 已知直线 $m / / n$ ，将一块含 $30 °$ 角的直角三角板 $A B C$ 按如图方式放置（ $∠ A B C = 30 °$ ），其中 $A$ ， $B$ 两点分别落在直线 $m$ ， $n$ 上，若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
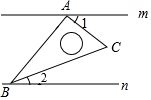6. 如图，AB是⊙O的直径，CD是弦，∠BCD=30°，OA=2，则阴影部分的面积是（）

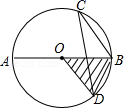A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、π D、2π

查看试题解析
7. 若关于x的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则实数k的取值范围是（）

A、 $k > - 1$ B、 $k > - 1$ 且 $k \neq 0$ C、 $k < - 1$ D、 $k < - 1$ 或 $k = 0$

查看试题解析
8. 若关于x的一元一次不等式组 ${\begin{array}{l} x - \frac{1}{4} (4 a - 2) \leq \frac{1}{2} \\ \frac{3 x - 1}{2} < x + 2 \end{array}$ 的解集是x $\leq$ a，且关于y的分式方程 $\frac{2 y - a}{y - 1} - \frac{y - 4}{1 - y} = 1$ 有非负整数解，则符合条件的所有整数a的和为（）

A、0 B、1 C、4 D、6

查看试题解析
9. 如图，已知在▱ABCD中，E为AD的中点，CE的延长线交BA的延长线于点F，则下列选项中的结论错误的是（）

A、FA：FB=1：2 B、AE：BC=1：2 C、BE：CF=1：2 D、S_△_ABE：S_△_FBC=1：4

查看试题解析
10. 如图，已知A，B两点的坐标分别为(8，0)，(0，8)，点C，F分别是直线 $x = - 5$ 和 $x$ 轴上的动点， $C F = 10$ ，点D是线段 $C F$ 的中点，连接 $A D$ 交 $y$ 轴于点E，当 $Δ A B E$ 面积取得最小值时， $\tan ∠ B A D$ 的值是（）

A、 $\frac{8}{17}$ B、 $\frac{4 \sqrt{2}}{17}$ C、 $\frac{4 \sqrt{2}}{13}$ D、 $\frac{7}{17}$

查看试题解析

二、填空题

11. 一组数据4，1，7，4，5，6则这组数据的极差为.

查看试题解析
12. 若分式 $\frac{4 x - 1}{x^{2} + 1}$ 的值为0，则 $x =$ .

查看试题解析
13. 分解因式：xy²﹣2xy+x= ．

查看试题解析
14. 《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？设有x匹大马，y匹小马，根据题意可列方程组为．

查看试题解析
15. 如图，将等腰直角三角形ABC（∠B=90°）沿EF折叠，使点A落在BC边的中点A₁处，BC=8，那么线段AE的长度为.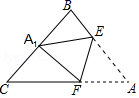

查看试题解析
16. 位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间，周边风景秀丽.随着年代的增加，目前塔底低于地面约7米.某校学生先在地面 $A$ 处侧得塔顶的仰角为30°，再向古塔方向行进 $a$ 米后到达 $B$ 处，在 $B$ 处侧得塔顶的仰角为45°(如图所示)，已知古塔的整体高度约为40米，那么 $a$ 的值为米.(结果保留根式)

查看试题解析
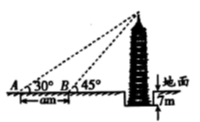17. 如图，在▱ABCD中，AD=7，AB=2 $\sqrt{3}$ ，∠B=60°.E是边BC上任意一点，沿AE剪开，将△ABE沿BC方向平移到△DCF的位置，得到四边形AEFD，则四边形AEFD周长的最小值为.

查看试题解析
18. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $B C = 12$ ， $D$ 为 $A C$ 边的中点，线段 $B D$ 的垂直平分线分别与边 $B C$ ， $A B$ 交于点 $E$ ， $F$ ，连接 $D F$ ， $E F$ .设 $B E = x$ ， $\tan ∠ A C B = y$ .给出以下结论：① $D F / / B C$ ；② $Δ B D E$ 的面积为 $\frac{3}{2} x y$ ；③ $Δ C D E$ 的周长为 $12 + x$ ；④ $x^{2} - y^{2} = 9$ ；⑤ $2 x - y^{2} = 9$ .其中正确结论有(把你认为正确结论的序号都填上).

查看试题解析

三、解答题

19. 计算: ${(- \frac{1}{2})}^{- 2} + | 2 - \sqrt{3} | + {(π - 1)}^{0} + \sqrt{12}$ .

查看试题解析
20. 先化简，再求值： $\frac{1}{x^{2} + 2 x + 1} \cdot (1 + \frac{3}{x - 1}) \div \frac{x + 2}{x^{2} - 1}$ ，其中x=2 $\sqrt{5}$ ﹣1．

查看试题解析
21. 有四张正面分别标有数字0，1，2，3的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上洗均匀.

(1)、随机抽出一张卡片，则抽到数字“2”的概率为；

(2)、随机抽出一张卡片，记下数字后放回并搅匀，再随机抽出一张卡片，请用列表或画树状图的方法，求两次抽出的卡片上的数字之和是3的概率.

查看试题解析
22. 本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动。校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如下图所示：

根据以上信息，解答下列问题：

(1)、补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为 ▲ ；

(2)、求本次所抽取学生四月份“读书量”的平均数；

(3)、已知该校七年级有1200名学生，请你估计该校七年级学生中，四月份“读书量”为5本的学生人数。

查看试题解析
23. 某服装店用4500元购进一批衬衫，很快售完，服装店老板又用2100元购进第二批该款式的衬衫，进货量是第一次的一半，但进价每件比第一批降低了10元．

(1)、这两次各购进这种衬衫多少件？

(2)、若第一批衬衫的售价是200元/件，老板想让这两批衬衫售完后的总利润不低于1950元，则第二批衬衫每件至少要售多少元？

查看试题解析
24. 如图， $▱ O A B C$ 的边 $O A$ 在 $x$ 轴的正半轴上， $O A = 5$ ，反比例函数 $y = \frac{m}{x}$ ( $x > 0$ )的图象经过点 $C (1 ， 4)$ .

(1)、求反比例函数的关系式和点 $B$ 的坐标，

(2)、过 $A B$ 的中点 $D$ 作 $D P / / x$ 轴交反比例函数图象于点P，连接 $C P ， O P$ .求△ $Δ C O P$ 的面积.

查看试题解析
25. 甲、乙两车分别从 $A ， B$ 两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地，乙车匀速前往A地.设甲、乙两车距A地的路程为y(千米)，甲车行驶的时间为x(小时)，y与x之间的函数图象如图所示.

(1)、图中， $m =$ ， $n =$ ；

(2)、求甲车返回时y与x之间的函数关系式，并写出自变量x的取值范围；

(3)、在甲车返回到A地的过程中，当x为何值时，甲、乙两车相距190千米?

查看试题解析
26. 如图，四边形 $A B C D$ 内接于⊙ $O$ ， $A B = A C$ ， $B D ⊥ A C$ ，垂足为E.

(1)、若 $∠ B A C = 40 °$ ，则 $∠ A D C =$ °.

(2)、求证： $∠ B A C = 2 ∠ D A C$ ；

(3)、若 $A B = 10$ ， $C D = 5$ ，求 $B C$ 的值.

查看试题解析
27. 如1，在平面直角坐标系中，直线 $M N$ 分别与x轴、y轴交于点 $M (6 ， 0) ， N (0 ， 2 \sqrt{3})$ ，等边 $Δ A B C$ 的顶点B与原点O重合， $B C$ 边落在x轴正半轴上，点A恰好落在线段 $M N$ 上，将等边 $Δ A B C$ 从图1的位置沿x轴正方向以每秒1个单位长度的速度平移，边 $A B ， A C$ 分别与线段 $M N$ 交于点 $E ， F$ (如图2所示)，设 $Δ A B C$ 平移的时间为 $t$ (s).

(1)、 $∠ O M N =$ ，等边 $Δ A B C$ 的边长为；

(2)、在运动过程中，当 $t$ 为何值时，MN垂直平分AB；

(3)、在 $Δ A B C$ 开始平移的同时，点P从 $Δ A B C$ 的顶点B出发，以每秒2个单位长度的速度沿折线 $B A - A C$ 运动，当点P运动到C时立即停止运动， $Δ A B C$ 也随之停止平移.
①当点P在线段 $B A$ 上运动时，若 $A E = 2 P E$ ，求t的值；

②当点P在线段 $A C$ 上运动时，若 $Δ P E F$ 的面积 $\frac{\sqrt{3}}{4}$ ，求 $t$ 的值.

查看试题解析
28. 如图，已知抛物线 $y = a x^{2} + b x + c$ 的图象经过点 $A (0 ， 3)$ ， $B (1 ， 0)$ ，其对称轴为直线l： $x = 2$ ，过点 $A$ 作 $A C / / x$ 轴交抛物线于点C， $∠ A O B$ 的平分线交线段 $A C$ 于点E，点P是抛物线上的一个动点，设其横坐标为m.

(1)、求抛物线的解析式；

(2)、如图1，动点P在直线 $B C$ 下方的抛物线上，连结 $P O ， P C$ ，当m为何值时，四边形 $O P C E$ 面积最大，并求出其最大值，

(3)、如图②， $F$ 是抛物线的对称轴 $l$ 上的一点，连接 $P O ， P F ， O F$ ，在抛物线x轴下方的图象上是否存在点 $P$ 使 $△ P O F$ 满足：① $∠ O P F = 90 °$ ；② $\tan ∠ P O F = \frac{1}{2}$ ？若存在，求点P的坐标，若不存在，请说明理由.

查看试题解析