江苏省南京市浦口区2020年数学中考二模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 命名为2019-nCoV的新型冠状病毒的大小约125纳米,即0.000 000 125米.用科学记数法表示0.000 000 125是( ).A、125×10–7 B、1.25×10–7 C、1.25×10–6 D、125×10–92. 计算(-2x2yz)3的结果是( )A、8x6y3z3 B、-8x5y3 z3 C、-6x6y3z3 D、-8x6y3z33. 下列运算中,结果最小的是( )A、1-(-2) B、1-|-2| C、1×(-2) D、1÷(-2)4. 实数a,b,c,d在数轴上的对应点的位置如图所示,则下列结论正确的是( )
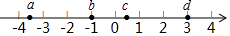 A、|a|>|b| B、a>﹣3 C、a>﹣d D、5. 下列无理数中,与4最接近的是( )A、 B、 C、 D、6. 如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到 .若反比例函数 的图象恰好经过 的中点D,则k的值是( )
A、|a|>|b| B、a>﹣3 C、a>﹣d D、5. 下列无理数中,与4最接近的是( )A、 B、 C、 D、6. 如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到 .若反比例函数 的图象恰好经过 的中点D,则k的值是( )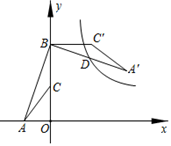 A、9 B、12 C、15 D、18
A、9 B、12 C、15 D、18二、填空题
-
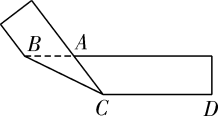
7. - 的相反数是; 的倒数是.8. 计算 - 的结果是.9. 分解因式:4a2-64=.10. 若方程 的两根 ,则 的值为.11. 将一个矩形 纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD=.
12. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN,若AB=9,BE=6,则MN的长为.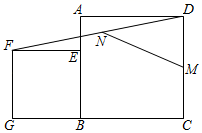 13. 为了解某区初中学生对网络游戏的喜好和作业量多少情况,随机抽取了该区500名同学进行了调查,并将调查的情况进行了整理,如下表:
13. 为了解某区初中学生对网络游戏的喜好和作业量多少情况,随机抽取了该区500名同学进行了调查,并将调查的情况进行了整理,如下表:作业量多少
网络游戏的喜好
认为作业多
认为作业不多
合计
喜欢网络游戏
180
90
270
不喜欢网络游戏
80
150
230
根据抽样调查结果,估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是.
14. 如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是°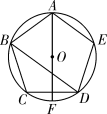 15. “低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路汽骑车匀速前往甲地,两人之间的距离s(km)与出发时间t(h)之间的函数关系如图中折线段AD-DE-EF所示,则E点坐标为
15. “低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路汽骑车匀速前往甲地,两人之间的距离s(km)与出发时间t(h)之间的函数关系如图中折线段AD-DE-EF所示,则E点坐标为.
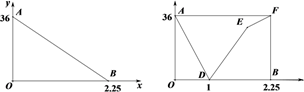 16. 如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则2AD+3BD的最小值是.
16. 如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则2AD+3BD的最小值是.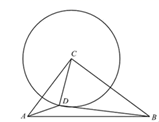
三、解答题
-
17. 计算(2a-b+1)(2a-1-b)18. 解不等式组 ,并写出它的所有非负整数解.19. 丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
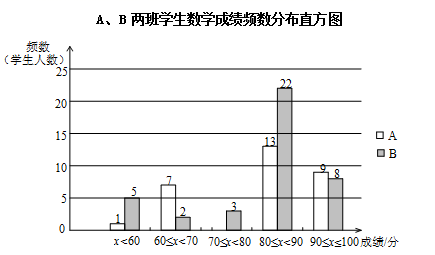
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数
中位数
方差
A班
80.6
m
96.9
B班
80.8
n
153.3
根据以上信息,回答下列问题:
(1)、补全数学成绩频数分布直方图;(2)、写出表中m、n的值;(3)、请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).20. 一个不透明的布袋中仅有2个红球、1个黑球,这些球除颜色外无其他差别.(1)、甲同学先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是多少?(2)、乙同学从中一次摸出两个球,则摸出的小球均为红色的概率是.21. 货车行驶25千米与汽车行驶35千米所用时间相同,已知汽车每小时比货车多行驶20千米,求两车的速度各为多少?22. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使CF=BE,连接DF. (1)、求证:四边形AEFD是矩形;(2)、若BF=8,DF=4,求CD的长.23. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55 m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1 m.参考数据:tan34°≈0.67,tan60°= 1.73)
(1)、求证:四边形AEFD是矩形;(2)、若BF=8,DF=4,求CD的长.23. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55 m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1 m.参考数据:tan34°≈0.67,tan60°= 1.73)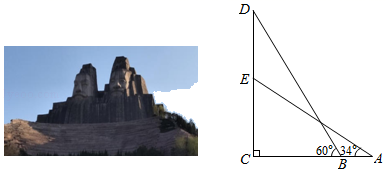 24. 如图,点 在半径为8的 上,过点 作 ,交 延长线于点 .连接 ,且 .
24. 如图,点 在半径为8的 上,过点 作 ,交 延长线于点 .连接 ,且 . (1)、求证: 是 的切线;(2)、求图中阴影部分的面积.25. 随着 技术的发展,人们对各类 产品的使用充满期待.某公司计划在某地区销售第一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 ( 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.
(1)、求证: 是 的切线;(2)、求图中阴影部分的面积.25. 随着 技术的发展,人们对各类 产品的使用充满期待.某公司计划在某地区销售第一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 ( 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.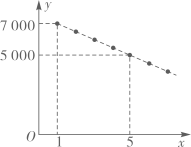 (1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?26. 在平面直角坐标系xOy中,已知抛物线y=x2﹣mx+n.(1)、当m=2时,
(1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?26. 在平面直角坐标系xOy中,已知抛物线y=x2﹣mx+n.(1)、当m=2时,①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;
②若点A(﹣2,y1),B(x2 , y2)都在抛物线上,且y2>y1 , 求x2的取值范围;
(2)、已知点P(﹣1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.27. 如图1,在矩形ABCD中,BC=3,动点P从B出发,以每秒1个单位的速度,沿射线BC方向移动,作△PAB关于直线PA的对称△PAB' ,设点P的运动时间为t(s).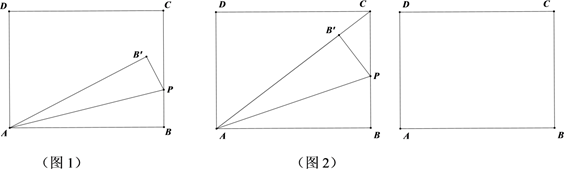 (1)、若AB=2 .
(1)、若AB=2 .①如图2,当点B' 落在AC上时,求t的值;
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t值?若不存在,请说明理由.
(2)、若四边形ABCD是正方形,直线PB'与直线CD相交于点M,当点P不与点C重合时,求证:∠PAM=45°.