江苏省高邮市2020年数学中考模拟试卷(5月)
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 如图,是小明同学在数轴上标注了这组数中 的两个无理数的位置,则这组数从小到大排列正确的是( )
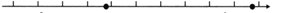 A、 B、 C、 D、2. 下列说法正确的是( )A、﹣1的绝对值的平方根是1 B、0的平方根是 0 C、 是最简二次根式 D、( )﹣3等于3. 下列事件:
A、 B、 C、 D、2. 下列说法正确的是( )A、﹣1的绝对值的平方根是1 B、0的平方根是 0 C、 是最简二次根式 D、( )﹣3等于3. 下列事件:①掷一次骰子,向上一面的点数是3;②从一个只装有黑色球的袋子摸出一个球,摸到的是白球;③13个人中至少有两个人的生日是在同一个月份;④射击运动员射击一次,命中靶心;⑤水中捞月;⑥冬去春来.其中是必然事件的有( )
A、1个 B、2个 C、3个 D、4个4. 如图,a∥b,点B在直线b上,且AB⊥BC,∠1=36°,那么∠2=( )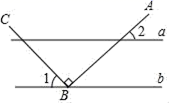 A、54° B、56° C、44° D、46°5. 将A(﹣4,1)向右平移5个单位,再向下平移2个单位,平移后点的坐标是( )A、(﹣9,3) B、(1,﹣1) C、(﹣9,1) D、(1,3)6. 如图,直线 分别与x轴、y轴交于点 ,直线 分别与x轴、y轴交于点 ,直线 与直线 相交于点 ,则不等式 的解集为( )
A、54° B、56° C、44° D、46°5. 将A(﹣4,1)向右平移5个单位,再向下平移2个单位,平移后点的坐标是( )A、(﹣9,3) B、(1,﹣1) C、(﹣9,1) D、(1,3)6. 如图,直线 分别与x轴、y轴交于点 ,直线 分别与x轴、y轴交于点 ,直线 与直线 相交于点 ,则不等式 的解集为( )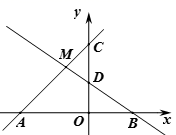 A、 B、 C、 D、7. 下列函数中,图象经过坐标原点的是( )A、 B、 C、 D、8. 如图,在正方形 中,顶点 在坐标轴上,且 ,以 为边构造菱形 .将菱形 与正方形 组成的图形绕点 逆时针旋转,每次旋转 ,则第2020次旋转结束时,点 的坐标为( )
A、 B、 C、 D、7. 下列函数中,图象经过坐标原点的是( )A、 B、 C、 D、8. 如图,在正方形 中,顶点 在坐标轴上,且 ,以 为边构造菱形 .将菱形 与正方形 组成的图形绕点 逆时针旋转,每次旋转 ,则第2020次旋转结束时,点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 科学家发现 冠状肺炎病毒颗粒平均直径约为 ,数据0.00000012用科学记数法表示.10. 体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位: )的最大值为186,最小值为155.若取组距为3,则可以分成组.11. 如果用s表示路程(单位:千米),t表示时间(单位:小时),v表示速度(单位:千米/时),那么t=时(用s和v表示).12. 下图是由六个棱长为 的正方体组成的几何体,则从上面看得到的平面图形的面积是.
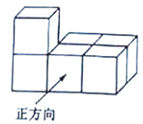 13. 在实数范围内分解因式:x4﹣9= .14. 已知:2m=12,2n=48,试计算:(﹣3)m﹣n=.15. 已知关于x的不等式(2a﹣b)x>a﹣2b的解是 ,则关于x的不等式ax+b<0的解为.16. 比较大小:tan30° cos30°(用“>”或“<”填空)17. 关于x的一元二次方程x2+4x﹣2k=0有实数根,则k的取值范围是.18. 如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为.
13. 在实数范围内分解因式:x4﹣9= .14. 已知:2m=12,2n=48,试计算:(﹣3)m﹣n=.15. 已知关于x的不等式(2a﹣b)x>a﹣2b的解是 ,则关于x的不等式ax+b<0的解为.16. 比较大小:tan30° cos30°(用“>”或“<”填空)17. 关于x的一元二次方程x2+4x﹣2k=0有实数根,则k的取值范围是.18. 如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为.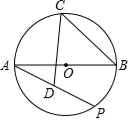
三、解答题
-
19. 计算:
(1)、2tan45°-( -1)0+ ;(2)、(a+2b)2-(a+b) (a-b).20. 解不等式(1)、解不等式组 的整数解.(2)、21. 移动支付快捷高效,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种,移动支付支付方式,为此在某步行街,使用某app,软件对使用移动支付的行人进行随机抽样调查,设置了四个选项,支付宝,微信,银行卡,其他移动支付(每人只选一项),以下是根据调查结果分别整理的不完整的条形统计图和扇形统计图.

请你根据下列统计图提供的信息,完成下列问题.
(1)、这次调查的样本容量是;(2)、请补全条形统计图;(3)、求在此次调查中表示使用微信支付的扇形所对的圆心角的度数.(4)、若某天该步行街人流量为10万人,其中40%的人购物并选择移动支付,请你依据此次调查获得的信息,估计一下当天使用银行卡支付的人数.22. 市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.(1)、甲同学随机选择连续的两天,其中有一天是星期三的概率是;(2)、乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)23. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?24. 如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕. (1)、求CM的长;(2)、求梯形ABCE的面积.25. 如图,AB为⊙O的直径,D是 的中点,BC与AD,OD分别交于点E,F.
(1)、求CM的长;(2)、求梯形ABCE的面积.25. 如图,AB为⊙O的直径,D是 的中点,BC与AD,OD分别交于点E,F.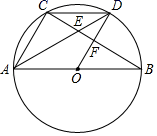 (1)、求证:OD∥AC;(2)、求证:DC2=DE•DA;(3)、若⊙O的直径AB=10,AC=6,求BF的长.26. 平面直角坐标系中,A(a,0),B(0,b),a,b满足 ,将线段AB平移得到CD,A,B的对应点分别为C,D,其中点C在y轴负半轴上.
(1)、求证:OD∥AC;(2)、求证:DC2=DE•DA;(3)、若⊙O的直径AB=10,AC=6,求BF的长.26. 平面直角坐标系中,A(a,0),B(0,b),a,b满足 ,将线段AB平移得到CD,A,B的对应点分别为C,D,其中点C在y轴负半轴上.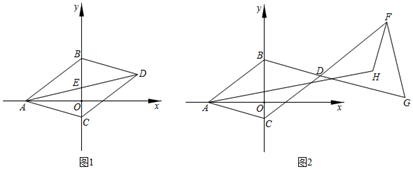 (1)、求A,B两点的坐标;(2)、如图1,连AD交BC于点E,若点E在y轴正半轴上,求 的值;(3)、如图2,点F,G分别在CD,BD的延长线上,连结FG,∠BAC的角平分线与∠DFG的角平分线交于点H,求∠G与∠H之间的数量关系.27. 如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+ x+ (a为常数,a<0).
(1)、求A,B两点的坐标;(2)、如图1,连AD交BC于点E,若点E在y轴正半轴上,求 的值;(3)、如图2,点F,G分别在CD,BD的延长线上,连结FG,∠BAC的角平分线与∠DFG的角平分线交于点H,求∠G与∠H之间的数量关系.27. 如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+ x+ (a为常数,a<0).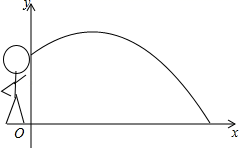 (1)、解释上述函数表达式中“ ”的实际意义;(2)、当a=﹣ 时,这名运动员能把铅球推出多远?(3)、若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.28. 如图1,△ABC是直角三角形,∠ACB=90°,点D在AC上,DE⊥AB于E,连接BD,点F是BD的中点,连接EF,CF.
(1)、解释上述函数表达式中“ ”的实际意义;(2)、当a=﹣ 时,这名运动员能把铅球推出多远?(3)、若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.28. 如图1,△ABC是直角三角形,∠ACB=90°,点D在AC上,DE⊥AB于E,连接BD,点F是BD的中点,连接EF,CF. (1)、EF和CF的数量关系为;(2)、如图2,若△ADE绕着点A旋转,当点D落在AB上时,小明通过作△ABC和△ADE斜边上的中线CM和EN,再利用全等三角形的判定,得到了EF和CF的数量关系,请写出此时EF和CF的数量关系;(3)、若△AED继续绕着点A旋转到图3的位置时,EF和CF的数量关系是什么?写出你的猜想,并给予证明.
(1)、EF和CF的数量关系为;(2)、如图2,若△ADE绕着点A旋转,当点D落在AB上时,小明通过作△ABC和△ADE斜边上的中线CM和EN,再利用全等三角形的判定,得到了EF和CF的数量关系,请写出此时EF和CF的数量关系;(3)、若△AED继续绕着点A旋转到图3的位置时,EF和CF的数量关系是什么?写出你的猜想,并给予证明.