江西省新余市2016-2017学年高一下学期理数期末考试试卷

试卷更新日期：2017-09-22 类型：期末考试

进入出卷网下载

一、选择题

1. 当输入x=﹣ $\frac{π}{6}$ 时，如图的程序运行的结果是（）

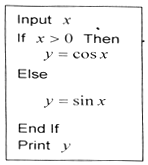A、﹣ $\frac{\sqrt{3}}{2}$ B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 设角θ的终边经过点P（﹣3，4），那么sinθ+2cosθ=（）

A、 $\frac{1}{5}$ B、 $- \frac{1}{5}$ C、 $- \frac{2}{5}$ D、 $\frac{2}{5}$

查看试题解析
3. 学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n的样本，其频率分布直方图如图所示，其中支出在[50，60）元的同学有30人，则n的值为（）

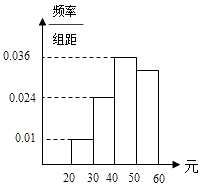A、300 B、200 C、150 D、100

查看试题解析
4. 过点（﹣1，3）且平行于直线x﹣2y+3=0的直线方程为（）

A、x﹣2y+7=0 B、2x+y﹣1=0 C、x﹣2y﹣5=0 D、2x+y﹣5=0

查看试题解析
5. 某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1～200编号，并按编号顺序平均分为40组抽出的号码为28，则第8组抽出的号码应是a；若用分层抽样方法，则50岁以下年龄段应抽取b人，那么a+b等于（）

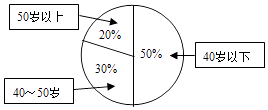A、46 B、45 C、70 D、69

查看试题解析
6. 在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{1}{5}$ C、 $\frac{1}{10}$ D、 $\frac{1}{12}$

查看试题解析
7. 阅读如图程序框图，运行相应的程序，则程序运行后输出的结果为（）

A、7 B、9 C、10 D、11

查看试题解析
8. 在△ABC中，∠ABC=120°，BA=2，BC=3，D，E是线段AC的三等分点，则 $\vec{B D}$ • $\vec{B E}$ 的值为（）

A、 $\frac{65}{9}$ B、 $\frac{11}{9}$ C、 $\frac{41}{9}$ D、﹣ $\frac{13}{9}$

查看试题解析
9. 已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜π），且函数的图象如图所示，则点（ω，φ）的坐标是（）

A、 $(2 ， \frac{2 π}{3})$ B、 $(4 ， \frac{2 π}{3})$ C、 $(2 ， \frac{π}{3})$ D、 $(4 ， \frac{π}{3})$

查看试题解析
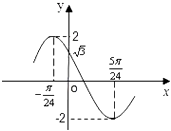10. 已知O为△ABC内一点，且 $\vec{A O} = \frac{1}{2} (\vec{O B} + \vec{O C})$ ， $\vec{A D} = t \vec{A C}$ ，若B，O，D三点共线，则t的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
11. 定义在R上的偶函数f（x），满足f（x+1）=f（x﹣1），且f（x）在[﹣3，﹣2]上是增函数，又α、β是锐角三角形的两个内角，则（）

A、f（sinα）＞f（cosβ） B、f（cosα）＜f（cosβ） C、f（sinα）＜f（cosβ） D、f（sinα）＜f（sinβ）

查看试题解析
12. 已知向量 $\vec{O A} ， \vec{O B}$ 满足 $\vec{| O A |} = \vec{| O B |} = 1 ， \vec{O A} ⊥ \vec{O B} ， \vec{O C} = λ \vec{O A} + μ \vec{O B} (λ ， μ \in R)$ ，若M为AB的中点，并且 $| \vec{M C} | = 1$ ，则λ+μ的最大值是（）

A、 $1 - \sqrt{3}$ B、 $1 + \sqrt{2}$ C、 $\sqrt{5}$ D、 $1 + \sqrt{3}$

查看试题解析

二、填空题

13. 已知tanα=3，则 $\frac{2 s i n α - c o s α}{s i n α + 3 c o s α}$ = ．

查看试题解析
14. 已知扇形的周长是4cm，面积是1cm² ，则扇形的圆心角的弧度数是．

查看试题解析
15. 已知| $\vec{a}$ |=4， $\vec{e}$ 为单位向量，当 $\vec{a}$ 、 $\vec{e}$ 的夹角为 $\frac{2 π}{3}$ 时， $\vec{a}$ + $\vec{e}$ 在 $\vec{a}$ ﹣ $\vec{e}$ 上的投影为．

查看试题解析
16. 对于函数f（x）= ${\begin{matrix} s i n π x ， x \in [0 ， 2] \\ \frac{1}{2} f (x - 2) ， x \in (2 ， + \infty) \end{matrix}$ ，有下列5个结论：
①任取x₁ ， x₂∈[0，+∞），都有|f（x₁）﹣f（x₂）|≤2；
②函数y=f（x）在区间[4，5]上单调递增；
③f（x）=2kf（x+2k）（k∈N₊），对一切x∈[0，+∞）恒成立；
④函数y=f（x）﹣ln（x﹣1）有3个零点；
⑤若关于x的方程f（x）=m（m＜0）有且只有两个不同实根x₁ ， x₂ ，则x₁+x₂=3．
则其中所有正确结论的序号是．（请写出全部正确结论的序号）

查看试题解析

三、解答题

17. 已知向量 $\vec{a}$ 、 $\vec{b}$ 满足| $\vec{a}$ |=1，| $\vec{b}$ |=2， $\vec{a}$ 与 $\vec{b}$ 的夹角为60°．

(1)、若（k $\vec{a}$ ﹣ $\vec{b}$ ）⊥（ $\vec{a}$ + $\vec{b}$ ），求k的值；

(2)、若|k $\vec{a}$ ﹣ $\vec{b}$ |＜2，求k的取值范围．

查看试题解析
18. 大学生赵敏利用寒假参加社会实践，对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查，销售单价x元和销售量y件之间的一组数据如表所示：
月份
7
8
9
10
11
销售单价x元
9
9.5
10
10.5
11
销售量y件
11
10
8
6
5

(1)、根据7至11月份的数据，求出y关于x的回归直线方程；

(2)、预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？
参考公式：回归直线方程 $\hat{y}$ =b $\hat{x}$ +a，其中b= $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ．
参考数据： $\sum_{i = 1}^{5} x_{i} y_{i}$ =392， $\sum_{i = 1}^{5} x_{i}^{2}$ =502.5．

查看试题解析
19. 设向量 $\vec{a}$ =（sinx， $\sqrt{3}$ cosx）， $\vec{b}$ =（﹣1，1）， $\vec{c}$ =（1，1），其中x∈（0，π]．

(1)、若（ $\vec{a}$ + $\vec{b}$ ）∥ $\vec{c}$ ，求实数x的值；

(2)、若 $\vec{a}$ • $\vec{b}$ = $\frac{1}{2}$ ，求函数sinx的值．

查看试题解析
20. 设关于x的一元二次方程x²+ax﹣ $\frac{b^{2}}{4}$ +1=0．

(1)、若a是从1，2，3这三个数中任取的一个数，b是从0，1，2这三个数中任取的一个数，求上述方程中有实根的概率；

(2)、若a是从区间[0，3]中任取的一个数，b是从区间[0，2]中任取的一个数，求上述方程有实根的概率．

查看试题解析
21. 已知函数f（x）= $\sqrt{3}$ sinxcosx﹣cos²x+ $\frac{1}{2}$ ，（x∈R）．

(1)、若对任意x∈[﹣ $\frac{π}{12}$ ， $\frac{π}{2}$ ]，都有f（x）≥a，求a的取值范围；

(2)、若先将y=f（x）的图象上每个点纵坐标不变，横坐标变为原来的2倍，然后再向左平移 $\frac{π}{6}$ 个单位得到函数y=g（x）的图象，求函数y=g（x）﹣ $\frac{1}{3}$ 在区间[﹣2π，4π]内的所有零点之和．

查看试题解析
22. 已知 $\vec{a}$ =（sinx，cosx）， $\vec{b}$ =（sinx，k）， $\vec{c}$ =（﹣2cosx，sinx﹣k）．

(1)、当x∈[0， $\frac{π}{4}$ ]时，求| $\vec{b}$ + $\vec{c}$ |的取值范围；

(2)、若g（x）=（ $\vec{a}$ + $\vec{b}$ ）• $\vec{c}$ ，求当k为何值时，g（x）的最小值为﹣ $\frac{3}{2}$ ．

查看试题解析

月份	7	8	9	10	11
销售单价x元	9	9.5	10	10.5	11
销售量y件	11	10	8	6	5