初中数学浙教版八年级上册第一章 三角形的初步知识 单元检测（提高篇）
试卷更新日期：2020-07-22 类型：单元试卷
一、单选题
-
1. 下列命题为假命题的是（ ）.A、三条边分别对应相等的两个三角形全等 B、三角形的一个外角大于与它相邻的内角 C、角平分线上的点到角两边的距离相等 D、等边三角形的三条角平分线、三条中线、三条高分别交于一点2. 能说明命题“对于任何实数a，|a|>-a”是假命题的一个反例可以是（ ）A、a=-2 B、a= C、a=1 D、a=3. 如图，A，B，C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1BlC1的面积是（ ）
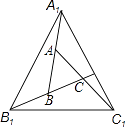A、4 B、5 C、6 D、74. 已知△ABC的两条中线的长分别为5、10，若第三条中线的长也是整数，则第三条中线长的最大值（ ）A、7 B、8 C、14 D、155. 长为1的一根绳，恰好可围成两个全等三角形，则其中一个三角形的最长边x的取值范围为（ ）A、 B、 C、 D、6. 如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC=BC，则下列选项正确的是（ ）A、
B、
C、
D、
7. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点 G作EF ∥ BC交AB于E，交AC 于F，过点G作 GD⊥AC 于D，下列四个结论：① EF=BE+CF；②∠BGC=90°+ ∠A ；③点G到 △ABC 各边的距离相等；④设GD=m，AE+AF=n，则
=mn. 其中正确的结论有（ ） 
A、1个 B、2个 C、3个 D、4个8. 如图，在△ABC中，BD、CE分别是∠ABC和∠ACB的平分线，AM⊥CE于P，交BC于M，AN⊥BD于Q，交BC于N，∠BAC=110°，AB=6，AC=5，MN=2，结论①AP=MP；②BC=9；③∠MAN=35°；④AM=AN.其中不正确的有（ ）
A、4个 B、3个 C、2个 D、1个二、填空题
-
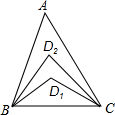
9. 如图，在△ABC中，∠A＝20°，∠ABC与∠ACB的平分线交于点D1 ， ∠ABD1与∠ACD1的平分线交于点D2 ， 以此类推，∠ABD2与∠ACD2的平分线交于点D ， 则∠BDC的度数是 ．
10. △ABC中，∠C=90°，∠A=20°，点O是AB的中点，将OB绕点O向三角形外部旋转α角时(0°<α<180°)，得到OP，当△ACP为等腰三角形时，α的值为。11. 如图，△ABC的三边AB、BC、CA的长分别为30、40、15，点P是三条角平分线的交点，将△ABC分成三个三角形，则 ︰ ︰ 等于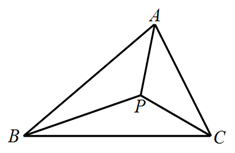
12. 如图，在∠AOB 的边 OA、OB 上取点 M、N，连接 MN，P 是△MON 外角平分线的交点， 若 MN=2， ， ． 则△MON 的周长是；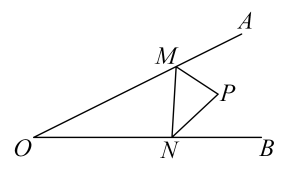
三、综合题
-
13. 按下列要求画图并填空：
(1)、过点B画出直线AC的垂线，交直线AC于点D ， 那么点B到直线AC的距离是线段的长.(2)、用直尺和圆规作出△ABC的边AB的垂直平分线EF，交边AB、AC于点M、N，联结CM.那么线段CM是△ABC的 .（保留作图痕迹）14. 如图，是一个4×4的方格，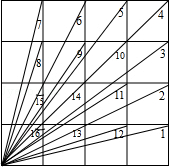
(1)、求图中∠1+∠2+∠3+∠4+…+∠16的和．(2)、求∠1﹣∠2+∠3﹣∠4+…+∠15﹣∠16．15. 生活常识：射到平面镜上的光线（入射光线）和变向后的光线（反射光线）与平面镜所夹的角相等.如图1，MN是平面镜，若入射光线AO与水平镜面夹角为∠1，反射光线OB与水平镜面夹角为∠2，则∠1=∠2.
(1)、现象解释：如图2，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD.已知：∠1=55°，求∠4的度数.(2)、尝试探究：如图3，有两块平面镜OM，ON，入射光线AB经过两次反射，得到反射光线CD，光线AB与CD相交于点E，若∠MON=46°，求∠CEB的度数.(3)、深入思考：如图4，有两块平面镜OM，ON，且∠MON=α，入射光线AB经过两次反射，得到反射光线CD，光线AB与CD所在的直线相交于点E，∠BED=β，α与β之间满足的等量关系是.（直接写出结果）16.(1)、如图①，AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系？为什么？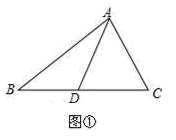
(2)、若三角形的面积记为S，例如：△ABC的面积记为S△ABC.如图②，已知S△ABC＝1.△ABC的中线AD、CE相交于点O，求四边形BDOE的面积.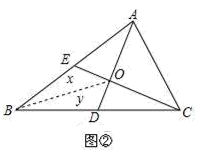
小华利用(1)的结论，解决了上述问题，解法如下：
连接BO，设S△BEO＝x，S△BDO＝y，由(1)结论可得：S△BCE＝S△BAD＝ S△ABC＝ ，S△BCO＝2S△BDO＝2y，S△BAO＝2S△BEO＝2x.则有 即 所以x＋y＝ .即四边形BDOE面积为 .
请仿照上面的方法，解决下列问题：
Ⅰ.如图③，已知S△ABC＝1.D、E是BC边上的三等分点，F、G是AB边上的三等分点，AD、CF交于点O，求四边形BDOF的面积.
Ⅱ.如图④，已知S△ABC＝1.D、E、F是BC边上的四等分点，G、H、I是AB边上的四等分点，AD、CG交于点O，则四边形BDOG的面积为.
17. 如图1，已知∠ACD是△ABC的一个外角，我们容易证明∠ACD＝∠A+∠B，即三角形的一个外角等于与它不相邻的两个内角的和.那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？
(1)、尝试探究：如图2，∠DBC与∠ECB分别为△ABC的两个外角，则∠DBC+∠ECB∠A+180°（横线上填＞、＜或＝）(2)、初步应用：如图3，在△ABC纸片中剪去△CED，得到四边形ABDE，∠1＝135°，则∠2－∠C＝.(3)、解决问题：如图4，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案.(4)、如图5，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，请利用上面的结论探究∠P与∠A、∠D的数量关系.18. 如图1，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形，并将添加的全等条件标注在图上.请你参考这个作全等三角形的方法，解答下列问题：
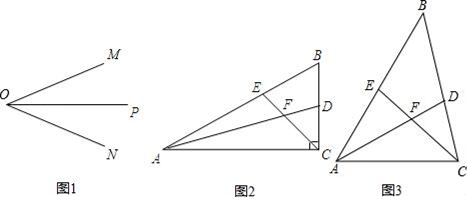(1)、如图2，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC和∠BCA的平分线，AD、CE相交于点F，求∠EFA的度数；(2)、在（1）的条件下，请判断FE与FD之间的数量关系，并说明理由；(3)、如图3，在△ABC中，如果∠ACB不是直角，而（1）中的其他条件不变，试问在（2）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由.19. 如图(1) ， ，BD⊥AB， ，点 在线段 上以 的速度由点 向点 运动，同时，点 在线段 上由点 向点 运动，它们运动的时间为 .
(1)、若点 的速度与点 的速度相等，当 时，求证： ；(2)、在(1)的条件下，判断此时 和 的位置关系，并证明；(3)、将图(1)中的“ ， ”，改为“ ”，得到图(2)，其他条件不变.设点 的运动速度为 ，请问是否存在实数 ，使得 与 全等？若存在，求出相应的 和 的值；若不存在，请说明理由.20. 为培育学生“敢进取”精神，特设计此题：
如图1，在 中， ，AC=BC， ， ，垂足分别为D，E.
(1)、若AD=2.5cm，DE=1.7cm，求BE的长.(2)、如图2，在原题其他条件不变的前提下，将CE所在直线旋转到 ABC的外部，请你猜想AD，DE，BE三者之间的数量关系，直接写出结论：.（不需证明）(3)、如图3，若将原题中的条件改为：“在 ABC中，AC=BC，D，C，E三点在同一条直线上，并且有 ，其中 为任意钝角”，那么（2）中你的猜想是否还成立？若成立，请予以证明；若不成立，请说明理由.