初中数学浙教版八年级上册第一章 三角形的初步知识 单元检测(基础篇)
试卷更新日期:2020-07-22 类型:单元试卷
一、单选题
-
1. 下列图形中与最右边图形全等的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下面四个图形中,线段BD是△ABC的高的图形是( )A、
2. 下面四个图形中,线段BD是△ABC的高的图形是( )A、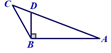 B、
B、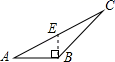 C、
C、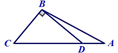 D、
D、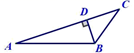 3. 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A、4 B、5 C、6 D、74. 下列命题中,是真命题的是( )A、无限小数是无理数 B、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 C、平行于同一条直线的两条直线平行 D、过一点有且只有一条直线与已知直线垂直5. 下列选项中,可以用来证明命题“若|a|>2,则a>2”是假命题的反例的是( )A、a=3 B、a=0 C、a=-2 D、a=-36. 如图,在△ABC中,∠B=70°,∠C=30°,则∠DAC的度数为( )
3. 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A、4 B、5 C、6 D、74. 下列命题中,是真命题的是( )A、无限小数是无理数 B、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 C、平行于同一条直线的两条直线平行 D、过一点有且只有一条直线与已知直线垂直5. 下列选项中,可以用来证明命题“若|a|>2,则a>2”是假命题的反例的是( )A、a=3 B、a=0 C、a=-2 D、a=-36. 如图,在△ABC中,∠B=70°,∠C=30°,则∠DAC的度数为( )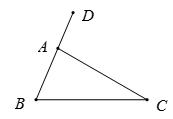 A、100° B、110° C、150° D、80°7. 下列是利用了三角形的稳定性的有( )
A、100° B、110° C、150° D、80°7. 下列是利用了三角形的稳定性的有( )①自行车的三角形车架:②校门口的自动伸缩栅栏门:③照相机的三脚架:④长方形门框的斜拉条
A、1个 B、2个 C、3个 D、4个8. 用一把带有刻度的直角尺,(1)可以画出两条平行线;(2)可以画出一个角的平分线;(3)可以确定一个圆的圆心.以上三个判断中正确的个数是( )A、0个 B、1个 C、2个 D、3个9. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )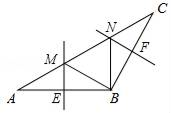 A、36 B、24 C、18 D、1610. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是
A、36 B、24 C、18 D、1610. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是 A、BC=EC,∠B=∠E B、BC=EC,AC=DC C、BC=DC,∠A=∠D D、∠B=∠E,∠A=∠D
A、BC=EC,∠B=∠E B、BC=EC,AC=DC C、BC=DC,∠A=∠D D、∠B=∠E,∠A=∠D二、填空题
-
11. 把命题“平行于同一直线的两条直线平行”写成“如果 , 那么”的形式.12. 已知△ABC≌△DEF,若∠B=40°,∠D=30°,则∠F=.13. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于 MN的长半径画弧,两弧交于点P,作射线AP,交边BC于点D,若CD=4,AB=15,则△ABD的面积是.
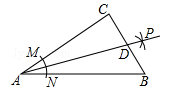 14. 如图,△ABC中,点E是BC上的一点,EC=3BE,点D是AC中点,若S△ABC=36,则S△ADF-S△BEF = .
14. 如图,△ABC中,点E是BC上的一点,EC=3BE,点D是AC中点,若S△ABC=36,则S△ADF-S△BEF = .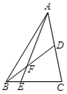 15. 如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是.
15. 如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是. 16. 如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于时,ΔABC和ΔPQA全等.
16. 如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于时,ΔABC和ΔPQA全等.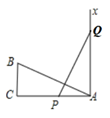
三、解答题
-
17. (用直尺和圆规作图)
已知:线段 ,求作: ,使 .
 18. 如图,点 , 在 的边 上, , ,求证: .
18. 如图,点 , 在 的边 上, , ,求证: .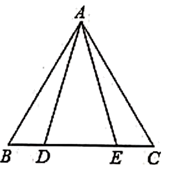 19. 如图,已知∠AOB=30°,P是∠AOB角平分线上一点,CP∥OA,交OB于点C,PD⊥OA,垂足为点D,且PC=4,求PD的长.
19. 如图,已知∠AOB=30°,P是∠AOB角平分线上一点,CP∥OA,交OB于点C,PD⊥OA,垂足为点D,且PC=4,求PD的长. 20. 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
20. 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.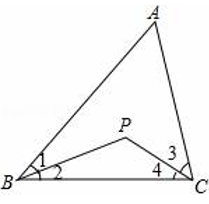 (1)、当∠A=40°,∠ABC=60°时,求∠BPC的度数;(2)、当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(1)、当∠A=40°,∠ABC=60°时,求∠BPC的度数;(2)、当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)、小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
21. 探究与发现:在△ABC中,∠B=∠C,点D在BC边上(点B、C除外),点E在AC边上,且∠ADE=∠AED,连接DE. (1)、如图①,若∠B=∠C=45º,
(1)、如图①,若∠B=∠C=45º,①当∠BAD=60º时,求∠CDE的度数;
②试猜想∠BAD与∠CDE的数量关系,并说明理由.
(2)、深入探究:如图②,若∠B=∠C,但∠C≠45º,其他条件不变,试探究∠BAD与∠CDE的数量关系.22. 已知:如图,点 在 的边 上,且 . (1)、求证: ;(2)、若 的平分线 交 于点 , 交 于点 ,设 , ,求 的长.23. 在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为8cm.
(1)、求证: ;(2)、若 的平分线 交 于点 , 交 于点 ,设 , ,求 的长.23. 在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为8cm.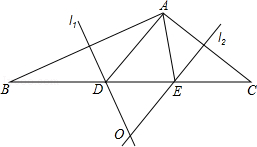 (1)、求BC的长;(2)、分别连结OA、OB、OC,若△OBC的周长为18cm,求OA的长.24. 如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E.
(1)、求BC的长;(2)、分别连结OA、OB、OC,若△OBC的周长为18cm,求OA的长.24. 如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E. (1)、如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;(2)、如图 2,若 BC=CD,求证:BD=2AE ;(3)、如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为.
(1)、如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;(2)、如图 2,若 BC=CD,求证:BD=2AE ;(3)、如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为.