初中数学浙教版八年级上册1.5 三角形全等的判定——SAS和线段垂直平分线 同步练习
试卷更新日期:2020-07-21 类型:同步测试
一、单选题
-
1. 如图,将两根钢条 AA',BB' 的中点连接在一起,使AA',BB' 可以绕着点O自由转动,就做成了一个测量工具(卡钳),则图中AB的长等于内槽宽 A′B′ ,那么判定 △OAB≌△OA′B′ 的理由是( )
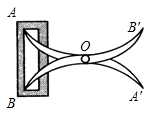 A、边角边 B、边边边 C、角边角 D、角角边2. 如图,在△ABC中,AB的垂直平分线交AC于点D , 交AB于点E , 如果 cm, cm,那么△ 的周长是( )
A、边角边 B、边边边 C、角边角 D、角角边2. 如图,在△ABC中,AB的垂直平分线交AC于点D , 交AB于点E , 如果 cm, cm,那么△ 的周长是( )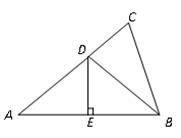 A、6 cm B、7 cm C、8 cm D、9 cm3. 如图,已知△ABC的三条角平分线交于点O,且∠BAC=120°,延长CA至点D,使DC=BC,连接OD,则∠BOD的度数为( )
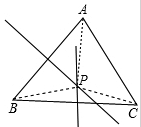
A、6 cm B、7 cm C、8 cm D、9 cm3. 如图,已知△ABC的三条角平分线交于点O,且∠BAC=120°,延长CA至点D,使DC=BC,连接OD,则∠BOD的度数为( ) A、45° B、50° C、60° D、75°4. 如图,在△ABC中,DE是边AC的垂直平分线,且分别交BC,AC干点D,E,连接AD,若∠B=70°,∠BAD=60°,则∠C为( )
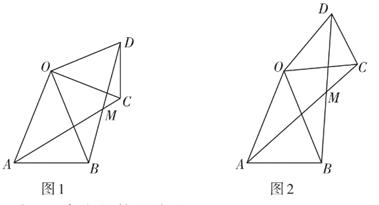
A、45° B、50° C、60° D、75°4. 如图,在△ABC中,DE是边AC的垂直平分线,且分别交BC,AC干点D,E,连接AD,若∠B=70°,∠BAD=60°,则∠C为( ) A、20° B、25° C、30° D、50°5. 如图, 是 的中线,E,F分别是 和 延长线上的点,且 ,连结 , .下列说法:① ;② 和 面积相等;③ ;④ .其中正确的有( )
A、20° B、25° C、30° D、50°5. 如图, 是 的中线,E,F分别是 和 延长线上的点,且 ,连结 , .下列说法:① ;② 和 面积相等;③ ;④ .其中正确的有( ) A、1个 B、2个 C、3个 D、4个6. 如图,D,E分别为△ABC的边AC,BC上的点,AE⊥BD,垂足为F,且AF=EF.若∠ABC=36°,∠C=44°,则∠EAC的度数为( )
A、1个 B、2个 C、3个 D、4个6. 如图,D,E分别为△ABC的边AC,BC上的点,AE⊥BD,垂足为F,且AF=EF.若∠ABC=36°,∠C=44°,则∠EAC的度数为( )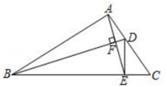 A、18° B、28° C、36° D、38°7. 有A,B,C三个社区(不在同一直线上),现准备修建一座公园,使该公园到三个社区的距离相等,那么公园应建在下列哪个位置上?( )A、△ABC三条角平分线的交点处 B、△ABC三条中线的交点处 C、△ABC三条高的交点处 D、△ABC三边垂直平分线的交点处8. 已知AD是△ABC中BC边上的中线,AB=4,AC=6,则AD的取值范围是( )A、2<AD<10 B、1<AD<5 C、4<AD<6 D、4≤AD≤6
A、18° B、28° C、36° D、38°7. 有A,B,C三个社区(不在同一直线上),现准备修建一座公园,使该公园到三个社区的距离相等,那么公园应建在下列哪个位置上?( )A、△ABC三条角平分线的交点处 B、△ABC三条中线的交点处 C、△ABC三条高的交点处 D、△ABC三边垂直平分线的交点处8. 已知AD是△ABC中BC边上的中线,AB=4,AC=6,则AD的取值范围是( )A、2<AD<10 B、1<AD<5 C、4<AD<6 D、4≤AD≤6二、填空题
-
9. 在△ABC中,边AB、BC、AC的垂直平分线相交于P,则PA、PB、PC的大小关系是.
 10. 如图,AB是线段CD的垂直平分线,若AC=5cm,BD=3cm,则四边形CADB的周长为cm.
10. 如图,AB是线段CD的垂直平分线,若AC=5cm,BD=3cm,则四边形CADB的周长为cm.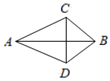 11. 如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=62°,则∠AEB= .
11. 如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=62°,则∠AEB= . 12. 在△ 中, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧分别交于点 ,作直线 交 于点 ,则 的度数是 .
12. 在△ 中, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧分别交于点 ,作直线 交 于点 ,则 的度数是 . 13. 如图,∠BAC=∠ABD,请你添加一个条件: , 能使△ABD≌△BAC(只添一个即可).
13. 如图,∠BAC=∠ABD,请你添加一个条件: , 能使△ABD≌△BAC(只添一个即可).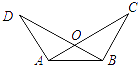 14. 如图所示, , , ,点 在线段 上,若 , ,则 .
14. 如图所示, , , ,点 在线段 上,若 , ,则 .
三、解答题
-
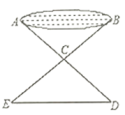
15. 如图,有一个池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接达到点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长度就是 , 的距离,为什么?