湖北省襄阳市樊城区2020年数学中考适应性卷

试卷更新日期：2020-07-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中，相反数是 $- \frac{1}{2}$ 的是（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. 下列运算正确的是（）

A、a³+a³＝2a⁶ B、a⁶÷a^﹣³＝a³ C、a³•a²＝a⁶ D、(﹣2a²)³＝﹣8a⁶

查看试题解析
3. 世界卫生组织通报说，沙特阿拉伯报告新增5例中东呼吸系统综合征冠状病毒（新型冠状病毒）确诊病例.全球新型冠状病毒确诊病例已达176例，其中死亡74例.冠状病毒颗粒的直径60-200nm，平均直径为100nm，新型冠状病毒直径为178nm，呈球形或椭圆形，具有多形性.如果1nm=10^-9米，那么新型冠状病毒的半径约为（）米

A、1.00×10^-7 B、1.78×10^-7 C、8.90×10^-8 D、5.00×10^-8

查看试题解析
4. 如图，AB//CD， EF⊥BD垂足为F，∠1=40°，则∠2的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
5. 如图，四边形ABCD是平行四边形，用直尺和圆规作∠BAD的平分线AG交BC于点E，若AB=5，BF=6，则AE的长为（）

A、8 B、10 C、11 D、12

查看试题解析
6. 下列立体图形中，主视图和左视图不一样的是（）

A、 B、 C、 D、

查看试题解析
7. 我国明代数学读本《算法统宗》一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托，如果一托为5尺，那么索长（）尺.

A、25 B、20 C、15 D、10

查看试题解析
8. 如图，从一块直径为 $2 m$ 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为（）

A、 $\frac{π}{2} m^{2}$ B、 $\frac{\sqrt{3}}{2} π m^{2}$ C、 $π m^{2}$ D、 $2 π m^{2}$

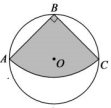查看试题解析
9. 下列关于一次函数 $y = k x + b (k < 0 ， b > 0)$ 的说法，错误的是（）

A、图象经过第一、二、四象限 B、 $y$ 随 $x$ 的增大而减小 C、图象与 $y$ 轴交于点 $(0 ， b)$ D、当 $x > - \frac{b}{k}$ 时， $y > 0$

查看试题解析
10. 二次函数y＝ax²+bx+c的图象如图所示，则反比例函数y＝﹣ $\frac{a}{x}$ 与一次函数y＝﹣bx+c在同一坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. $4^{2}$ 的算术平方根是.

查看试题解析
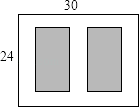
12. 在实数范围内分解因式：3x²﹣6＝．

查看试题解析
13. 重庆市某校初二（3）班同学，在学校组织的语文作文选拔考试中，有三名同学满分，其中有一名男生和两名女生，现在从三名满分同学中随机抽取两名同学参加重庆市优秀作文比赛，则选出来的两名同学刚好是一男一女的概率是.

查看试题解析
14. 如图，某小区有一块长为30m，宽为24m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480m² ，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为 m．

查看试题解析
15. 已知半径为10的⊙O中，弦 $A B = 10 \sqrt{2}$ ，弦AC=10，则∠BAC的度数是为

查看试题解析
16. 如图，E ， F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是．

查看试题解析

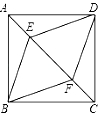
三、解答题

17. 先化简，再求值： $\frac{a^{2} - b^{2}}{a} \div (a - \frac{2 a b - b^{2}}{a})$ ，其中a=2+ $\sqrt{3}$ ，b=2- $\sqrt{3}$ .

查看试题解析
18. “五一”江北水城文化旅游期间，几名同学包租一辆面包车去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，求原来参加游览的同学有多少人？

查看试题解析
19. 某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表.

使用次数

0

1

2

3

4

5

人数

11

15

23

28

18

5

(1)、这天部分出行学生使用共享单车次数的中位数是，众数是.

(2)、这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）

(3)、若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少名.

查看试题解析
20. 如图，小明家的窗口到地面的距离 $C E = 9$ 米，他在C处测得正前方花园中树木顶部A点的仰角为37°，树木底部B点的俯角为45°，求树木 $A B$ 的高度．（参考数据： $\sin 37^{°} \approx 0.60$ ， $\cos 37^{°} \approx 0.80$ ， $\tan 37^{°} \approx 0.75$ ）

查看试题解析
21. 已知反比例函数y= $\frac{k}{x}$ 与一次函数y=ax+b的图象相交于点A（2，6），和点B（4，m）.

(1)、求反比例函数与一次函数的解析式；

(2)、直接写出不等式 $\frac{k}{x}$ ≤ax+b的解集和△AOB的面积.

查看试题解析
22. 如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC，BC于点D，E，点F在AC的延长线上，且∠BAC＝2∠CBF.

(1)、求证：BF是⊙O的切线；

(2)、若⊙O的直径为3，sin∠CBF＝ $\frac{\sqrt{3}}{3}$ ，求BC长.

查看试题解析
23. 某体育用品商场采购员要到厂家批发购买篮球和排球共 $100$ 个,篮球个数不少于排球个数，付款总额不得超过 $11200$ 元，已知两种球厂的批发价和商场的零售价如下表. 设该商场采购 $x$ 个篮球.

品名

厂家批发价/元/个

商场零售价/元/个

篮球

$120$

$150$

排球

$100$

$120$

(1)、求该商场采购费用 $y$ (单位:元)与 $x$ (单位:个)的函数关系式,并写出自变最 $x$ 的取值范围：

(2)、该商场把这 $100$ 个球全都以零售价售出,求商场能获得的最大利润；

(3)、受原材料和工艺调整等因素影响,采购员实际采购时，低球的批发价上调了 $3 m (m > 0)$ 元/个，同时排球批发价下调了 $2 m$ 元/个.该体有用品商场决定不调整商场零售价，发现将 $100$ 个球全部卖出获得的最低利润是 $2300$ 元,求 $m$ 的值.

查看试题解析
24. 已知：△ABC与△ABD中，∠CAB＝∠DBA＝β，且∠ADB＋∠ACB＝180°.

(1)、提出问题：如图1，当∠ADB＝∠ACB＝90°时，求证：AD＝BC；

(2)、类比探究：如图2，当∠ADB≠∠ACB时，AD＝BC是否还成立？并说明理由.

(3)、综合运用：如图3，当β＝18°，BC＝1，且AB⊥BC时，求AC的长.

查看试题解析
25.
如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线y=﹣x²+bx+c经过A，B两点，点P在线段OA上，从点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以 $\sqrt{2}$ 个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．

(1)、求抛物线的解析式；

(2)、当t为何值时，△APQ为直角三角形；

(3)、过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标．

查看试题解析

品名	厂家批发价/元/个	商场零售价/元/个
篮球	$120$	$150$
排球	$100$	$120$

使用次数	0	1	2	3	4	5
人数	11	15	23	28	18	5