湖北省荆门市2020年数学中考适应性卷

试卷更新日期：2020-07-21 类型：中考模拟

进入出卷网下载

一、选择题

1. $- | - \frac{1}{2} |$ 的相反数的倒数是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、2 D、 $- 2$

查看试题解析
2. 一种新病毒的半径仅有0.000009毫米，将0.000009用科学记数法表示应是（）

A、 $9 \times 10^{- 6}$ B、 $9 \times 10^{- 5}$ C、 $0.9 \times 10^{- 6}$ D、 $0.9 \times 10^{- 5}$

查看试题解析
3. 选择计算 $(- 4 x^{2} + 3 y) (4 x^{2} + 3 y)$ 的最佳方法是（）

A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式

查看试题解析
4. 如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（）

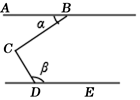A、∠α+∠β＝95° B、∠β﹣∠α＝95° C、∠α+∠β＝85° D、∠β﹣∠α＝85°

查看试题解析
5. 图2是图1中长方体的三视图，若用S表示面积，S_主＝x²+2x ， S_左＝x²+x ，则S_俯＝（）

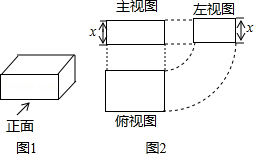A、x²+3x+2 B、x²+2 C、x²+2x+1 D、2x²+3x

查看试题解析
6. 如图，在 $R t Δ A B C$ 中， $∠ B = 90^{\circ}$ ，以点 $A$ 为圆心，适当长为半径画弧，分别交 $A B 、 A C$ 于点 $D ， E$ ，再分别以点 $D 、 E$ 为圆心，大于 $\frac{1}{2} D E$ 为半径画弧，两弧交于点 $F$ ，作射线 $A F$ 交边 $B C$ 于点 $B G = 1 ， A C = 4$ ，则 $Δ A C G$ 的面积是（）

A、 $1$ B、 $\frac{3}{2}$ C、 $2$ D、 $\frac{5}{2}$

查看试题解析
7. 若一次函数 $y = k x + b$ 的图象不经过第二象限，则关于 $x$ 的方程 $x^{2} + k x + b = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
8. 已知点A（-1， $\sqrt{3}$ ），O为坐标原点，连接OA.将线段OA绕点O按逆时针方向旋转 $30 °$ 得到线段 $O A^{'}$ ，则点 $A^{'}$ 的坐标为（）

A、 $(1$ ， $- \sqrt{3})$ B、 $(- 2$ ， $\sqrt{3})$ C、 $(- \sqrt{3}$ ， $2)$ D、 $(- \sqrt{3}$ ， $1)$

查看试题解析
9. 为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则这组数据的中位数和众数分别是（）

阅读量（单位：本/周）

0

1

2

3

人数（单位：人）

1

4

6

4

A、1，2 B、2，2 C、4，6 D、6，6

查看试题解析
10. 已知分式方程 $\frac{x + 3}{x + 2} = \frac{k}{(x - 1) (x + 2)} + 1$ 的解为非负数，求k的取值范围（）

A、 $k \geq 5$ B、 $k \geq - 1$ C、 $k \geq 5$ 且 $k \neq 6$ D、 $k \geq - 1$ 且 $k \neq 0$

查看试题解析
11. 已知一扇形的圆心角为 $60 °$ ，半径为5，则以此扇形为侧面的圆锥的底面圆的周长为（）

A、 $\frac{5}{3} π$ B、 $10 π$ C、 $\frac{5}{6} π$ D、 $\frac{1}{6} π$

查看试题解析
12. 已知抛物线y＝ax²+3x+c（a，c为常数，且a≠0）经过点（﹣1，﹣1），（0，3），有下列结论：①ac＜0；②当x＞1时，y的值随x值的增大而减小；③3是方程ax²+2x+c＝0的一个根；④当﹣1＜x＜3时，ax²+2x+c＞0其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 计算： $\sqrt{12} - 3 \tan 30 ° + {(π - 2020)}^{0} - {(\frac{1}{2})}^{- 1} =$ .

查看试题解析
14. 若关于 $x$ 的一元二次方程 $x^{2} + (m - 2) x + m^{2} = 0$ 的两个实数根互为倒数，则 $m$ 的值是.

查看试题解析
15. 如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点C，交OB于点D，若OA＝4，则阴影部分的面积为.

查看试题解析
16. 如图，已知直线 $y = \frac{\sqrt{3}}{3} x + 2$ 与x轴，y轴分别交于点A，B，将△ABO沿直线AB翻折后得到△ABC，若反比例函数 $y = \frac{k}{x}$ （x＜0）的图象经过点C，则k＝.

查看试题解析
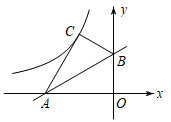17. 如图，在正方形ABCD中，M、N是对角线AC上的两个动点，P是正方形四边上的任意一点，且 $A B = 4$ ， $M N = 2$ .关于下列结论：①当△PAN是等腰三角形时，P点有6个；②当△PMN是等边三角形时，P点有4个；③DM+DN的最小值等于6.其中，一定正确的结论的序号是.

查看试题解析

三、解答题

18. 先化简（1﹣ $\frac{3}{x + 2}$ ）÷ $\frac{x^{2} - 2 x + 1}{x^{2} - 4}$ ，然后从不等式2x﹣6＜0的非负整数解中选取一个合适的解代入求值．

查看试题解析
19.

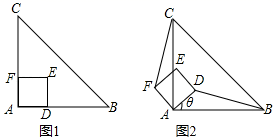(1)、问题发现：如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，点D、F分别在边AB、AC上，请直接写出线段BD、CF的数量和位置关系；

(2)、拓展探究：如图2，当正方形ADEF绕点A逆时针旋转锐角θ时，上述结论还成立吗？若成立，请给予证明；若不成立，请说明理由.

查看试题解析
20. 为提升学生的艺术素养，学校计划开设四门艺术选修课：A．书法；B．绘画；C．乐器；D．舞蹈．为了解学生对四门功课的喜欢情况，在全校范围内随机抽取若干名学生进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．将数据进行整理，并绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：

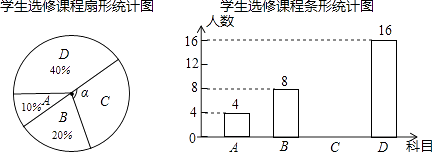(1)、本次调查的学生共有多少人？扇形统计图中∠α的度数是多少？

(2)、请把条形统计图补充完整；

(3)、学校为举办2018年度校园文化艺术节，决定从A．书法；B．绘画；C．乐器；D．舞蹈四项艺术形式中选择其中两项组成一个新的节目形式，请用列表法或树状图求出选中书法与乐器组合在一起的概率．

查看试题解析
21. 如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i（即tan∠ABC）为1： $\sqrt{3}$ ，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC.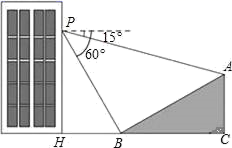

(1)、求出山坡坡角（∠ABC）的大小；

(2)、求A、B两点间的距离（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.732）.

查看试题解析
22. 如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P.

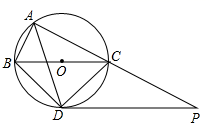(1)、求证：PD是⊙O的切线；

(2)、求证： $A B \cdot C P = B D \cdot C D$ ；

(3)、若 $\tan ∠ A B C = 2$ ， $A B = 2 \sqrt{5}$ ，求线段DP的长.

查看试题解析
23. 随着《流浪地球》的热播，其同名科幻小说的销量也急剧上升.为应对这种变化，某网店分别花20000元和30000元先后两次增购该小说，第二次的数量比第一次多500套，且两次进价相同.

(1)、该科幻小说第一次购进多少套？

(2)、根据以往经验：当销售单价是25元时，每天的销售量是250套；销售单价每上涨1元，每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y（套）与销售单价x（元）之间的函数关系式及自变量x的取值范围；

②网店决定每销售1套该科幻小说，就捐赠a（0＜a＜7）元给困难职工，每天扣除捐赠后可获得的最大利润为1960元，求a的值.

查看试题解析
24. 如图，在平面直角坐标系中，菱形ABCD的三个顶点A，B，D在坐标轴上，且已知点A（ $- 3$ ， $0$ ），点B（ $0$ ， $4$ ），现有抛物线m经过点B，C和OD的中点.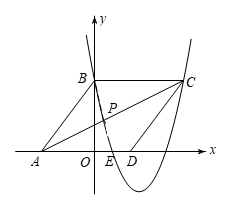

(1)、求抛物线m的解析式；

(2)、在抛物线 $m$ 上是否存在点P，使得 $S_{△ P B C} = S_{△ P D C}$ ？若存在，求出点P的坐标，若不存在，请说明理由；

(3)、抛物线m与x轴的另一交点为F，M是线段AC上一动点，求 $\sqrt{5} M F + M C$ 的最小值.

查看试题解析

阅读量（单位：本/周）	0	1	2	3
人数（单位：人）	1	4	6	4