湖北省黄石市2020年数学中考模拟试卷(5月)
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题
-
1. 下列四个数:﹣2,﹣0.6, , 中,绝对值最小的是( )A、﹣2 B、﹣0.6 C、 D、2. 全球新冠肺炎确诊人数截止到4月30日止约有220万人,用科学记数法表示220万人为( )A、220×104人 B、2.20×107人 C、2.20×106人 D、0.220×107人3. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
4. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )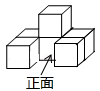 A、
A、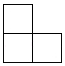 B、
B、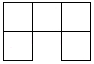 C、
C、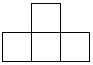 D、
D、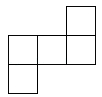 5. 化简5(2x﹣3)﹣4(3﹣2x)之后,可得下列哪一个结果( )
5. 化简5(2x﹣3)﹣4(3﹣2x)之后,可得下列哪一个结果( )
A、2x﹣27 B、8x﹣15 C、12x﹣15 D、18x﹣276. 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、7. 如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )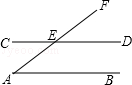 A、 35° B、 40° C、 45° D、 50°8. 二次函数 (a≠0)的图象如图所示,则下列结论中正确的是( )
A、 35° B、 40° C、 45° D、 50°8. 二次函数 (a≠0)的图象如图所示,则下列结论中正确的是( ) A、a>0 B、当﹣1<x<3时,y>0 C、c<0 D、当x≥1时,y随x的增大而增大9. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点 ,则 和 的面积之差 为( )
A、a>0 B、当﹣1<x<3时,y>0 C、c<0 D、当x≥1时,y随x的增大而增大9. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点 ,则 和 的面积之差 为( ) A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最小值是( )
A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最小值是( )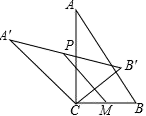 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 在实数范围内分解因式:x4﹣9= .12. 解分式方程: ,则方程的根是.13. 周末,张三、李四两人在磁湖游玩,张三在湖心岛 处观看李四在湖中划船(如图),小船从 处出发,沿北偏东 方向划行200米到 处,接着小船向正南方向划行一段时间到 处.在 处李四观测张三所在的 处在北偏西 的方向上,这时张三与李四相距米(保留根号).
 14. 从n个苹果和4个雪梨中,任选1个,若选中苹果的概率是 ,则n的值是.15. 如图,一个半径为 的圆形纸片在边长为 的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是.
14. 从n个苹果和4个雪梨中,任选1个,若选中苹果的概率是 ,则n的值是.15. 如图,一个半径为 的圆形纸片在边长为 的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是. 16. 一列数按某规律排列如下: , , , , , , , , , ,…,可写为: ,( , ),( , , ),( , , , ),…,若第n个数为 ,则n=.
16. 一列数按某规律排列如下: , , , , , , , , , ,…,可写为: ,( , ),( , , ),( , , , ),…,若第n个数为 ,则n=.三、解答题
-
17. 计算: ﹣(3.14﹣π)0﹣|3﹣ |﹣2cos30°.18. 先化简,再求代数式 的值,其中x=tan45°.19. 若关于x、y的二元一次方程组 的解满足x+y<2,求a的正整数解.20. 分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1 , x2.(1)、求m的取值范围.(2)、若|x1|=|x2|,求m的值及方程的根.21. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
 (1)、求证:CE=CF;(2)、若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?22. 在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
(1)、求证:CE=CF;(2)、若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?22. 在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.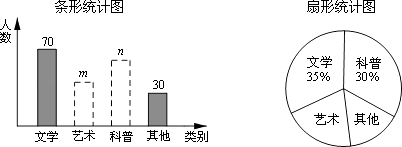
请你根据统计图提供的信息,解答下列问题:
(1)、本次调查中,一共调查了名同学;(2)、条形统计图中,m= , n=;(3)、扇形统计图中,艺术类读物所在扇形的圆心角是度;(4)、学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?23. 为了迎接“5.1”小长假的购物高峰,大冶雨润某运动品牌服装店准备购进甲、乙两种服装,已知每件甲服装进价比每件乙服装进价多20元,售价在进价的基础上加价50%,通过初步预算,若以4800元购进的甲服装比以4200元购进乙服装的件数少10件.(1)、求甲、乙两种服装的销售单价.(2)、现老板计划购进两种服装共100件,其中甲种服装不少于65件,若购进这100件服装的费用不超过7500元,则甲种服装最多购进多少件?24. 如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.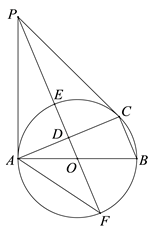
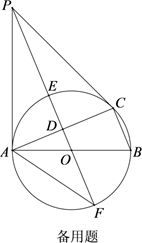 (1)、求证:PA是⊙O的切线;(2)、证明: ;(3)、若BC=8,tan∠AFP= ,求DE的长.
(1)、求证:PA是⊙O的切线;(2)、证明: ;(3)、若BC=8,tan∠AFP= ,求DE的长.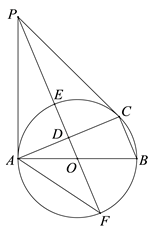 25. 如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒 个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
25. 如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒 个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.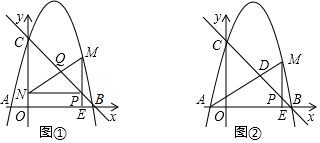 (1)、求抛物线的解析式;(2)、如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当 时,求t的值;(3)、如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.
(1)、求抛物线的解析式;(2)、如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当 时,求t的值;(3)、如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.