浙江省绍兴市新昌县2020年数学中考模拟试卷（5月）
试卷更新日期：2020-07-21 类型：中考模拟
一、选择题（本大题有10小题，每小题4分，共40分.请选出每小题中一个最符合题意的正确选项，不选、多选、错选，均不给分）
-
1. -2的相反数等于（ ）A、2 B、-2 C、 D、2. 新昌古称剡东，又名石城，建县于后梁开平二年（908年），全县面积约为1 213 000 000平方米，有着“东南眉目”之美誉，是浙江省十大养生福地之一，数字1 213 000 000用科学记数法可简洁表示为（ ）A、12.13×108 B、0.1213×1010 C、1.213×109 D、1.213×1083. 如图放置的几何体，它的主视图是（ ）
A、
B、
C、
D、
4. 一个不透明的袋子中有3个白球、2个黄球和1个红球，这些球除颜色外其他完全相同，那么从袋子中随机摸出一个球是黄球的概率为（ ）A、 B、 C、 D、5. 下列运算正确的是（ ）A、2a+2a=2a² B、a²·a3=a6 C、（-3a4）²=-9a8 D、a6÷a²=a46. 直线y=-2x+6与两坐标轴围成的三角形的面积是（ ）A、8 B、6 C、9 D、27. 如图为一座房屋屋架结构示意图，已知屋檐AB=BC，横梁EF∥AC，点E为AB的中点，且BD⊥EF，屋架高BD=4m，横梁AC=12m，则支架DF长为（ ）
A、2 B、2 C、 D、28. 如图，这条花边中有4个圆和4个正三角形，且这条花边的总长度AB为4，则花边上正三角形的内切圆半径为（ ）
A、 B、 C、1 D、9. 如图， 在平面直角坐标系中， 矩形O ABC的点B坐标为（8， 6） ，点A在x轴上，点C在y轴上.点D是边AB上的动点，连接OD，作点A关于线段OD的对称点A'.已知一条抛物线y=ax²+bx+c（a≠0）经过O，A'，A三点，且点A'恰好是抛物线的顶点，则b的值为（ ）
A、- B、2 C、-2 D、10. 小华用一罐黑漆和一罐白漆来漆一些立方体积木，他打算把这些立方体的每一面漆成单一的黑色或白色，如图1和图2是两种不同的漆法，但图2可以经过翻折得到图3，所以图2和图3是相同的漆法.那么他能漆成互不相同的立方体的种数是（ ）
A、10种 B、8种 C、9种 D、6种二、填空题（本大题有6小题，每小题5分，共30分.）
-
11. 因式分解：a2-9=.12. 如图，已知AC是△ABC外接圆的直径，∠BDA=50°，则∠CAB等于度。
13. 《九章算术》第七卷“盈不足”中记载：“今有共买物，人出八，盈三；人出七，不足四。问人数、物价各几何？”译为：“今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又差4钱。问人数、物价各多少？”通过计算可知，共有人合伙购物。14. 在平面直角坐标系中，如果一个图形向右平移1个单位，再向上平移3个单位，称为一个变换，已知点A（1，-2），经过一个变换后对应点为A1 ， 经过2个变换后对应点为A2 ， …经过n个变换后对应点为An ， 则用含n的代数式表示点An的坐标为。15. 如图，点A在反比例函数y= （x>0）的图象上，点B在反比例函数y= （k<0）的图象上，且OA⊥OB，线段AB交反比例函数y= （x>0） 的图象于另一点C，连结OC。若点C为AB的中点，tan∠OCA= ，则k的值为。
16. 把边长为1的正方形纸片ABCD分割成如图的四块，其中点E，F分别为AD，CD的中点，四边形AHGE是菱形，用这四块纸片拼成四边形MNPQ（要求这四块纸片不重叠无缝隙），则四边形MNPQ的周长是。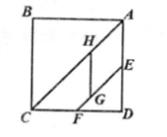
三、解答题（本大题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分.解答需写出必要的文字说明、演算步骤或证明过程。）
-
17.(1)、计算： +（ -1）0-2cos45°。(2)、解分式方程：18. 2020年突如其来的肺炎疫情，给我们的生活和学习带来了诸多不便.图1是2月1日至2月5日全国“新冠肺炎”疫情新增数据统计图，为了控制疫情蔓延扩散，国家全面落实疫情防控工作，举国上下众志成城，图2是3月5日至3月9日全国“新冠肺炎”疫情新增数据统计图，请根据统计图解答以下问题：
(1)、写出2月3日全国新增确诊病例数，并计算3月5日至3月9日全国新增确诊病例数的平均数。(2)、对比两幅统计图中的数据，选择一个角度分析评价此次疫情控制情况。19. 水龙头关闭不严会造成滴水，现用一个含有显示水量的圆柱形水杯接水做如图1的试验，研究水杯内盛水量w（L）与滴水时间t（h）的关系，根据试验数据绘制出如图2的函数图象，结合图象解答下列问题。
(1)、求w与t之间的函数关系式。(2)、若杯子容积为2.2L，计算杯子最多可以接多少时间的水？20. 某电工想换房间的灯泡，已知灯泡到地面的距离为2.65m，现有一架家用可调节式脚踏人字梯，其中踏板、地面都是水平的.梯子的侧面简化结构如图所示，左右支撑架长度相等，BD=1m。设梯子一边AD与地面的夹角为α，且α可调节的范围为60°≤α≤75°。当α=60°时，电工站在梯子安全档中最高一档踏板BE上的最大触及高度为2.60m。
(1)、当α=60°时，求踏板BE离地面的高度BH.（精确到0.01m）(2)、调节角度，试判断电工是否可以换下灯泡，并说明理由。（参考数据： ≈1.732，sin75°≈0.966，cos75°≈0.259，tan75°≈3.732）
21. 如图，以点O为旋转中心，将线段AB按顺时针方向旋转α得到线段A'B'，连结AA'，BB'。
(1)、比较∠OAA'与∠OBB'的大小，并说明理由。(2)、当α=45°时，若OA=3，OB=4；请你编制一个计算题（不标注新的字母），并解答（根据编出的问题层次，给不同的得分）。22. 如果一个直角三角形的三边长分别为a-d，a，a+d，（a>d>0），则称这个三角形为均匀直角三角形。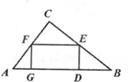
(1)、判定按照上述定义，下列长度的三条线段能组成均匀直角三角形的是（ ）。A、1，2，3 B、1， ，2 C、1， ，3 D、3，4，5(2)、性质求证：任何均匀直角三角形的较小直角边与较大直角边的比是3：4。(3)、应用如图，在一块均匀直角三角形纸板ABC中剪一个矩形，且矩形的一边在AB上，其余两个顶点分别在BC，AC上，已知AB=50cm，BC>AC，∠C=90°，求剪出矩形面积的最大值。23. 小明对教材“课题学习”中的“用一张正方形折出一个正八边形”的问题进行了认真的探索。他先把正方形ABCD沿对角线AC对折，再把∠BAC对折，使点B落在AC上，记为点E，然后沿CE的中垂线折叠，得到折痕PQ，如图1，类似地，折出其余三条折痕GH，IJ，KO，得到八边形GHIJKOPQ，如图2。
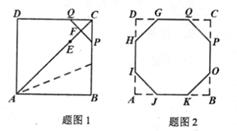(1)、求证：△CPQ是等腰直角三角形。(2)、若AB=a，求PQ的长。（用含a的代数式表示）(3)、我们把八条边长相等，八个内角都相等的八边形叫做正八边形.试说明八边形GHIJKOPQ是正八边形，请把过程补充完整。解：理由如下：
①
∴∠GQP=135°
同理可得：∠QPO=∠POK=∠OKJ=∠KJI=∠JIH=∠IHG=∠HGQ=135°。
②
∴PQ=QG。
同理可得：QG=GH=HI=IJ=JK=KO=PO=PQ
∴八边形GHIJKOPQ是正八边形。
24. 如图，在矩形ABCD中，已知AB=12，BC=16，点O是对角线AC的中点，点E是AD边上的动点，连结EO并延长交BC于点F，过O作GH⊥EF，分别交矩形的边于点G，H。
(1)、当H，F，G，E四点分别分布在矩形ABCD的四条边上（不包括顶点）时，①求证：四边形HFGE是菱形。
②求AE的取值范围。
(2)、当四边形HFGE的面积为144时，求AE的长。