浙江省嘉兴市秀洲区2020年数学中考二模试卷

试卷更新日期：2020-07-21 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分.请选出各题中唯一的正确选项，不选、多选、错选，均不得分）

1. -2020的倒数是（）

A、2020 B、-2020 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 下列计算，正确的是（）

A、a³·a²=a⁶ B、2a²-a=a C、a⁶÷a²=a³ D、（a³）²=a⁶

查看试题解析
3. 如图，线段AB两个端点的坐标分别为A（2，2）、B（3，1），以原点O为位似中心，在第一象限内将线段AB扩大为原来的2倍后得到线段CD，则端点C的坐标为（）

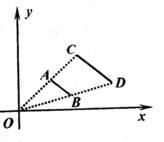A、（4，4） B、（3，3） C、（3，1） D、（4，1）

查看试题解析
4. 如图是由4个大小相同的正方体组合而成的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
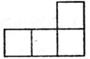
5. 已知a，b满足方程组 ${\begin{cases} 3 a + 2 b = 8 \\ 4 a + 5 b = 6 \end{cases}$ ，则a+b的值为（）

A、-4 B、4 C、-2 D、2

查看试题解析
6. 如图，数轴上的点A，B，O，C，D分别表示数-2，-1，0，1，2，则表示数2- $\sqrt{5}$ 的点P应落在（）

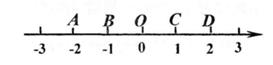A、线段AB上 B、线段BO上 C、线段OC上 D、线段CD上

查看试题解析
7. 如图，AB是⊙O的直径，C，D是⊙O上两点，且CD=CB，CD与AB交于点E，连接OD，若∠AOD=80°，则∠B的度数是（）

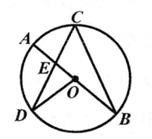A、20° B、25° C、30° D、35°

查看试题解析
8. 一组数据：3、4、4、5，若添加一个数据4，则发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
9. 如图，Rt△ABC中，∠ACB=90°，CD平分∠ACB交AB于点D，按下列步骤作图：

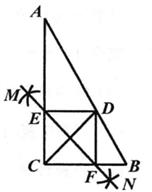
步骤1：分别以点C和点D为圆心，大于 $\frac{1}{2}$ CD的长为半径作弧，两弧相交于Ｍ，N两点；

步骤2：作直线MN，分别交AC，BC于点E，F；

步骤3：连接DE，DF。

若AC=4，BC=2，则线段DE的长为（）

A、 $\frac{5}{3}$ B、 $\frac{3}{2}$ C、 $\frac{4}{3}$ D、 $\sqrt{2}$

查看试题解析
10. 若抛物线y=-x²+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B.①抛物线y=-x²+2x+m+1与直线y=m+2有且只有一个交点；②若点M（-2，y₁）、点N（ $\frac{1}{2}$ ，y₂）、点P（2，y₃）在该函数图象上，则y₁<y₂<y₃；③将该抛物线向左平移2个单位，再向下平移2个单位，所得的抛物线解析式为y=-（x+1）²+m；④点A关于直线x=1的对称点为C，点D、E分别在x轴和y轴上，当m=1时，四边形BCDE周长的最小值为3+ $\sqrt{2}$ + $\sqrt{13}$ 。其中错误的是（）

A、①③ B、② C、②④ D、③④

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 分解因式：x²-4=。

查看试题解析
12. 据统计，嘉兴市2019年全市财政总收入达到94500000000元，列全省第三，94500000000用科学记数法可表示为。

查看试题解析
13. 若式子 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是。

查看试题解析

14. 为了解某区初中学生的视力情况，随机抽取了该区500名初中学生进行调查，整理样本数据，得到下表：根据抽样调查结果，估计该区12000名初中学生视力不低于4.8的人数是。

视力	4.7以下	4.7	4.8	4.9	4.9以上
人数	102	98	80	93	127

查看试题解析

15. 如图，在△ABC中，AC=BC=4 $\sqrt{2}$ ，∠C=90°，点D在BC上，且CD=3DB，将△ABC折叠，使点A与点D重合，EF为折痕，则tan∠BED的值是.

查看试题解析
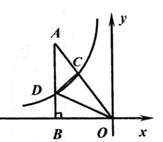
16. 如图，已知△OAB中，AB⊥OB，以O为原点，以BO所在直线为x轴建立坐标系。反比例函数的图象分别交AO，AB于点C，D，已知 $\frac{O C}{A C} = \frac{3}{2}$ ，△ACD的面积为 $\frac{16}{9}$ ，则该反比例函数的解析式为。

查看试题解析

三、解答题（本题有8小题，第17~19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）友情提醒：做解答题，别忘了写出必要的过程，作图（包括添加辅助线）最后必须用黑色字迹的签字笔或钢笔将线条描黑：

17. 计算：

(1)、（ $\sqrt{3}$ ）²+|-2|-（π-2）⁰

(2)、解不等式：3x-1≥2（x-1）

查看试题解析
18. 先化简，再求值：（3x+5）²-（3x-5）（3x+5），其中x= $- \frac{1}{2}$ 。

查看试题解析
19. 受新型冠状病毒疫情的影响，某市教育主管部门在推迟各级学校返校时间的同时安排各个学校开展形式多样的网络教学，学校计划在每周三下午15：30至16：30为学生提供以下四类学习方式供学生选择：在线阅读、微课学习、线上答疑、在线讨论，为了解学生的需求，通过网络对部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图。

(1)、求本次调查的学生总人数；

(2)、请求出“线上答疑”在扇形统计图中的圆心角度数；

(3)、笑笑和瑞瑞同时参加了网络学习，请求出笑笑和瑞瑞选择同一种学习方式的概率.

查看试题解析
20. 如图，⊙O与△ABC的边AC相切于点C，与边AB、BC分别交于点D、E，DE∥OA，CE是⊙O的直径。

(1)、求证：AB是⊙O的切线；

(2)、若BD=4，CE=6，求AC的长。

查看试题解析
21. 疫情期间部分学生选择在家用电视观看网络课程，为了保护眼睛，电视机的安装高度有一定的要求。如图所示，小嘉家的壁挂电视机的安装高度AB为1米，电视的中心位置D（AC的中点）比平视视线EF低8cm（这样观看眼睛最不容易疲劳），电视机宽度AC为60cm，眼到凳子平面的高度EH为75cm。

(1)、求小嘉应选用凳子的高度；

(2)、若看电视的视角∠CEF为3°时，观看感最好，求此时凳子中心H到墙AB的距离（电视机的厚度忽略不计）。（参考数据：sin3°≈0.0523，cos3°≈0.9997，tan3°≈0.0550）

查看试题解析
22. 如图，7×7的网格中，A，B，C均在格点上，请用无刻度的直尺作图（保留作图痕迹，不写作法）

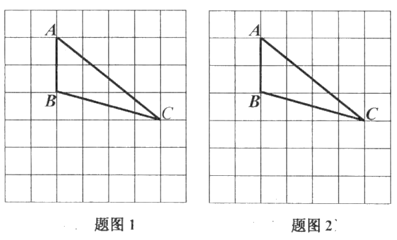(1)、在图1中找一格点D，使得△ACD为等腰三角形（找到一个即可）；

(2)、在图2中作出∠BAC的角平分线。

查看试题解析
23. 为了更好地做好复课准备，某班家委会讨论决定购买A，B两种型号的口罩供班级学生使用，已知A型口罩每包价格a元，B型口罩每包价格比A型少4元，180元钱购买的A型口罩比B型口罩少12包。

(1)、求a的值。

(2)、经与商家协商，购买A型口罩价格可以优惠，其中每包价格y（元）和购买数量x（包）的函数关系如图所示，B型口罩一律按原价销售。

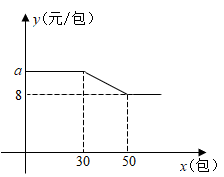
①求y关于x的函数解析式；

②若家委会计划购买A型、B型共计100包，其中A型不少于30包，且不超过60包。问购买A型口罩多少包时，购买口罩的总金额最少，最少为多少元？

查看试题解析
24. 我们定义：连结凸四边形一组对边中点的线段叫做四边形的“准中位线”.

(1)、概念理解：
如图1，四边形ABCD中，F为CD的中点，∠ADB=90°，E是AB边上一点，满足DE=AE，试判断EF是否为四边形ABCD的准中位线，并说明理由。

(2)、问题探究：
如图2，△ABC中，∠ACB=90°，AC=6，BC=8，动点E以每秒1个单位的速度，从点A出发向点C运动，动点F以每秒6个单位的速度，从点C出发沿射线CB运动，当点E运动至点C时，两点同时停止运动。D为线段AB上任意一点，连接并延长CD，射线CD与点A，B，E，F构成的四边形的两边分别相交于点M，N，设运动时间为t。问t为何值时，MN为点A，B，E，F构成的四边形的准中位线。

(3)、应用拓展：
如图3，EF为四边形ABCD的准中位线，AB=CD，延长FE分别与BA，CD的延长线交于点M，N，请找出图中与∠M相等的角并证明。

查看试题解析