浙江省台州市仙居县2020年（二模）数学试卷
试卷更新日期：2020-07-21 类型：中考模拟
一、选择题（本题有10小题，每题4分，共40分。）
-
1. 以下4个数中，是无理数的是（ ）A、2020 B、20.20020002 C、π D、0.2……2. 已知某个几何体的三视图分别为圆、长方形、长方形，则下列四个几何体中是该几何体的是（ ）A、圆锥体 B、圆柱体 C、球体 D、长方体3. 下列计算正确的是（ ）A、 B、（-x）2-x2=-x5 C、（-2x+y）（-2x-y）=4x2-y2 D、（x-2y）2=x2-4y24. 下列结论中，菱形具有而矩形不一定具有的性质是（ ）A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直5. 一个不透明的盒子里有n个除颜色外其他完全相同的小球，其中有9个黄球．每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么估计盒子中小球的个数n为（ ）A、20 B、24 C、28 D、306. 某书店分别用1000元和3000元两次购进某本小说，第二次数量比第一次多60套，两次进价相同，设该书店第一次购进x套，根据题意，列方程正确的是（ ）A、 B、 C、 D、7. 下列能和长度为3，4的两条线段组成锐角三角形的线段是（ ）A、7 B、6 C、5 D、48. 如图，AB是⊙O的直径，CD为弦，CD⊥AB且相交于点E，则下列结论中不成立的是（ ）
A、∠A=∠D B、CB=BD C、∠ACB=90° D、∠COB=3∠D9. 产品的价格是由市场价格波动产生的，而每种产品价格在当天是固定的，某采购商欲购A产品80件，B产品100件。甲供应商捆绑销售2件A产品和3件B产品，报价在400元~500元之间。乙供应商也捆绑销售3件A产品和2件B产品，报价在500元~600元之间。采购商打算从甲、乙供应商购进A产品80件，B产品100件，所要准备的资金为（ ）A、12600元~15200元之间 B、15200元~18800元之间 C、18800元~21600元之间 D、21600元~33000元之间10. 对于函数y=ax2-（2a+1）x-3a+1（a是常数），有下列说法：①函数图象与坐标轴总有三个不同的交点；
②当x<1时，不是y随x的增大而增大就是y随x的增大而减小；
③若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数。
其中错误的说法是（ ）
A、① B、①② C、②③ D、①③二、填空题（本题有6小题，每题5分，共30分）
-
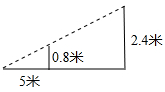
11. 分解因式： =.12. 一次函数y=-2x+4与x轴的交点坐标是。13. 小明在打网球时，为使球恰好能过网（网高0.8米），且落在对方区域离网5米的位置上，她的击球高度是2.4米，则她应站在离网的米处。
14. 在抗疫一线中，火神山医院的一间重症监护室一天需6名护士护理，两人一组，每4小时轮换，6名护士的编号分别是1号、2号、3号、4号、5号、6号，则1号和2号恰好在同一组的概率是15. 对于反比例函数y= ，当y<4且y≠0时，x的取值范围是。16. 如图的平面直角坐标系中，A点的坐标是（4，3）。图1中，点P为正方形ABCD的中心，顶点C、D分别在y轴和x轴的正半轴上，则OP=；图2中，点P为正△ABC的中心，顶点B、C分别在y轴和x轴的正半轴上，则OP=。
三、解答题（本题有8小题，第17~20题每题8分，第21题10分、第22、23题每题12分，第24题14分，共80分）
-
17. 计算：2-1+ -4sin60°18. 化简：（2m3）2+（2m）2-m（m3-1）19. 如图，这是一把可调节座椅的侧面示意图，已知头枕上的点A到调节器点O处的距离为80cm，AO与地面垂直。现调整靠背，把OA绕点O旋转35°到OA'处。求调整后点A'比调整前点A的高度降低多少厘米？（结果取整数）（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
20. 甲、乙两所学校选派相同人数的老师参加志愿者活动，参加活动时长分别被制成下列两个统计图，根据以上信息，整理分析数据如下表：平均时间/小时
中位数/小时
众数/小时
方差/小时2
甲
a
7
7
1.2
乙
7
b
8
c
(1)、求出表格中a，b，c的值；(2)、分别运用表中的统计量，简要分析这两所学校参加志愿者活动的时长，若选其中一所学校作为志愿推广学校，你认为应选哪所？21. 新房装修甲居民购买家居用品的清单如下表，因污水导致部分信息无法识别，据下表解决问题：家居用品名称
单价（元）
数量（个）
金额（元）
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术字画
a
2
90
电热水壶
35
1
b
合计
8
280
(1)、直接写出a= ， b=；(2)、甲居民购买了垃圾桶，塑料鞋架各几个？(3)、若甲居民再次购买艺术字画和垃圾桶两种家居用品，共花费150元，则有哪几种不同的购买方案？22. 如图1，Rt△ABC中，∠BCA=90°，BC=3，AC=4，直线AM⊥CA，点D是AC上的动点，过A、D、B三点的圆交纸线AM于点E，连DE。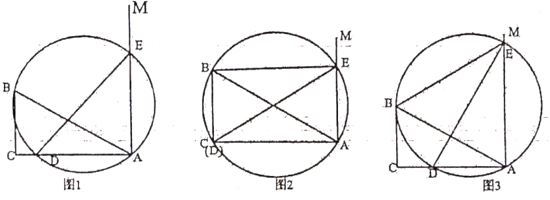
(1)、当点D与点C重合时如图2所示，连BE，求证：四边形AEBC是矩形；(2)、如图3，当CB与过A、D、B三点的圆相切时，求AD的长；(3)、作点A关于直线DE的对称点A'，试判断A'能否能落在直线CB上，若能请直接写出AD的长，若不能说明理由。23. 定义：每个内角都相等的八边形叫做等角八边形.容易知道，等角八边形的内角都等于135°，我们来研究它的一些性质与判定：
(1)、如图1，等角八边形ABCDEFGH中，连结BF。①请直接写出∠ABF+∠GFB的度数。
②求证：AB∥EF。
③我们把AB与EF称为八边形的一组正对边，由②同理可得：BC与FG，CD与GH，DE与HA这三组正对边也分别平行，请模仿平行四边形性质的学习经验，用一句话概括等角八边形的这一性质。
(2)、如图2，等角八边形ABCDEFGH中，如果有AB=EF，BC=FG，则其余两组正对边CD与GH，DE与HA分别相等吗？证明你的结论。(3)、如图3，八边形ABCDEFGH中，若四组正对边分别平行，则显然有∠A=∠E，∠B=∠F，∠C=∠G，∠D=∠H。请探究：该八边形至少需要已知几个内角为135°，才能保证它一定是等角八边形？24. 在长、宽均为45米的十字路口，现遇到红灯，有10辆车依次呈一直线停在路口的交通白线后，每二辆车间隔为2.5米，每辆车长5米。每辆车的速度v（米/秒）关于时间t（秒）的函数（如图1）所示。当绿灯亮起，第一辆车的车头与交通白线的距离s（米）关于时间t（秒）的函数解析式为s=a（t-1）2（1≤t≤4），（如图2）所示。当前车启动后，后面一辆车在1秒后也启动。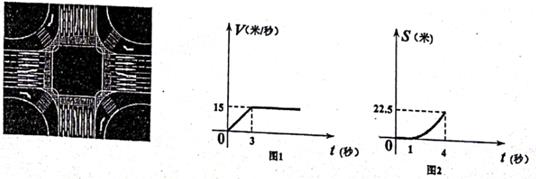
(1)、求a的值；(2)、当t>4时，求第一辆车的车头与交通白线的距离s（米）关于时间t（秒）的函数解析式；(3)、当t>4时，求第一辆车和第二辆车在这个十字路口中的最大间距（第一辆车的车尾和第二辆车车头）；(4)、绿灯持续时间至少要设置多长才能保证在绿灯期间这十辆车都能通过交通白线。