浙江省衢州市常山县2020年数学中考模拟试卷
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题(本题共10小题,每题3分,共30分)
-
1. 计算-1+2的值是( )A、-1 B、1 C、-3 D、32. 常山三衢石林是国家4A级旅游景区,占地面积约为27600000平方米,数据27600000用科学记数法表示为( )A、0.276×108 B、2.76×107 C、2.76×108 D、27.6×1063. 下列计算正确的是( )A、a3·a²=a5 B、a3÷a=a3 C、(a²)3=a5 D、(3a)3=3a34. 已知在Rt△ABC中,∠C=90°,AB=5,AC=3,则tanA的值( )A、 B、 C、 D、5. 计算 的结果为( )A、 B、 C、-1 D、26. 不等式组 的解在数轴上表示为( )A、
 B、
B、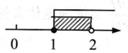 C、
C、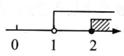 D、
D、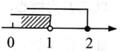 7. 甲、乙、丙、丁四人进行射击测试,成绩的平均数和方差如下表所示:
7. 甲、乙、丙、丁四人进行射击测试,成绩的平均数和方差如下表所示:平均数
8.9
8.7
8.6
8.9
方差
2.5
5.5
2.5
6.5
根据表中数据,要从中选一名成绩好又发挥稳定的选手参加比赛,则应该选择( )
A、甲 B、乙 C、丙 D、丁8. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )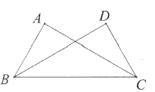 A、∠ABC=∠DCB B、∠A=∠D C、AC=DB D、AB=DC9. 如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为E,且BE:AE=1:4,则CD的长为( )
A、∠ABC=∠DCB B、∠A=∠D C、AC=DB D、AB=DC9. 如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为E,且BE:AE=1:4,则CD的长为( )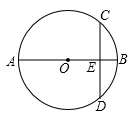 A、10 B、12 C、8 D、910. 如图1,一只蚂蚁从点O出发,以1厘米/秒速度沿着扇形AOB的边缘爬行一周。设爬行时间为x秒,蚂蚁到点O的距离为y厘米,y关于x的函数图象如图2所示,则扇形的面积为( )
A、10 B、12 C、8 D、910. 如图1,一只蚂蚁从点O出发,以1厘米/秒速度沿着扇形AOB的边缘爬行一周。设爬行时间为x秒,蚂蚁到点O的距离为y厘米,y关于x的函数图象如图2所示,则扇形的面积为( )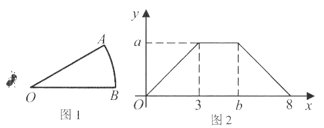 A、3 B、6 C、 π D、π
A、3 B、6 C、 π D、π二、填空题(本题共6小题,每题4分,共24分)
-
11. 分解因式:a2-4a=。12. 已知样本数据0,1,3,1,5,则这组数据的中位数是。13. 已知 ,则3a+b的值是。14. 已知二次函数y=ax²+bx+c自变量x的部分取值和对应函数值y如下表,则二次函数图象的对称轴是直线。
x
…
-4
-3
-1
1
2
3
…
y
…
21
13
3
1
3
7
…
15. 如图,在平面直角坐标系中,边长为2的正方形ABCD的顶点A与原点O重合,顶点B在直线l:y= x上,将正方形沿射线OB方向无滑动地翻滚.当正方形翻滚2020次点A对应点的坐标是 。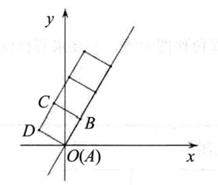 16. 如图,反比例函数y= (k>0)图象经过Rt△OAB直角边AB的中点C,与斜边OB相交于点D,过点D作DE⊥y轴于点E,连结CO,CD。
16. 如图,反比例函数y= (k>0)图象经过Rt△OAB直角边AB的中点C,与斜边OB相交于点D,过点D作DE⊥y轴于点E,连结CO,CD。 (1)、△ODE与△OAB的面积比为;(2)、若△COD的面积为1,则k的值为。
(1)、△ODE与△OAB的面积比为;(2)、若△COD的面积为1,则k的值为。三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分,请务必写出解答过程)
-
17. 计算: +( )-1-2tan45°+(2-π)018. 已知:如图,点A,F,E,C在同一条直线上,AB∥CD,且AB=CD,AE=CF。求证:四边形BEDF是平行四边形。19. 如图所示的直棱柱,其侧棱长为3cm,底面是边长为2cm的等边三角形。
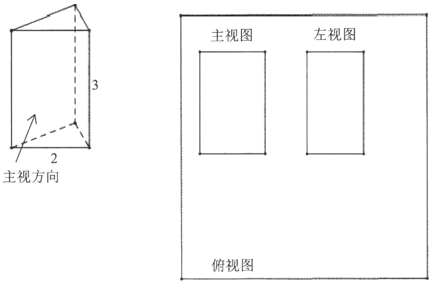 (1)、用尺规作图法补充完整它的三视图(保留作图痕迹,不要求写作法)。(2)、求该直棱柱左视图的面积。20. 新冠肺炎疫情在全球蔓延,截止2020年5月14日,我国确诊病例达84464例,为了解新冠肺炎的易感人群是否与年龄相关,从中随机抽取50名确诊病例,对其年龄进行统计,制成如下不完整频数表和频数直方图。
(1)、用尺规作图法补充完整它的三视图(保留作图痕迹,不要求写作法)。(2)、求该直棱柱左视图的面积。20. 新冠肺炎疫情在全球蔓延,截止2020年5月14日,我国确诊病例达84464例,为了解新冠肺炎的易感人群是否与年龄相关,从中随机抽取50名确诊病例,对其年龄进行统计,制成如下不完整频数表和频数直方图。50名确诊病例年龄频数表
年龄段(岁)
频数
0≤x<20
1
20≤x<40
12
40≤x<60
a
60≤x<80
15
80≤x<100
2

根据图表解决下列问题:
(1)、求表中a的值并补全频数直方图;(2)、从以上图表中写出两条相关的结论;(3)、小林、小敏响应社区号召,积极参加疫情联防联控工作,参与小区卡点值勤。某小区有A、B、C三个卡点,他们都可以从这三个卡点中任选一个参与值勤,求两人在同一卡点值勤的概率是多少(要求用列表法或画树状图求解)?21. 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F。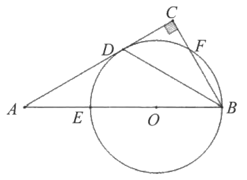 (1)、求证:AC是⊙O的切线;(2)、已知AB=6,BC=3,求 的长。22. 定义:有一组对角是直角,且夹其中一个直角的两边相等的四边形称为垂等四边形。
(1)、求证:AC是⊙O的切线;(2)、已知AB=6,BC=3,求 的长。22. 定义:有一组对角是直角,且夹其中一个直角的两边相等的四边形称为垂等四边形。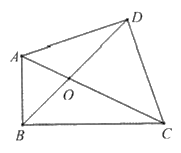 (1)、在矩形,菱形,正方形中,一定是垂等四边形的是。(2)、如图,在垂等四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,对角线AC与BD相交于点O。
(1)、在矩形,菱形,正方形中,一定是垂等四边形的是。(2)、如图,在垂等四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,对角线AC与BD相交于点O。①求证:BD平分∠ABC;
②若AB=2,BC=4,求BD的长。
23. 常山是“胡柚之乡”,小明经过市场调查发现,某乡柚农家中胡柚每月的销售量与售价关系如下表:售价x(元/箱)
80
90
100
110
…
月销量y(箱)
240
220
200
180
…
已知每箱胡柚的成本40元,设每箱胡柚的售价为x元。
(1)、每箱胡柚的销售利润是元(请用含x的式子表示);(2)、求月销量y与售价x的函数关系式;(3)、设销售胡柚的月利润为W元,那么每箱胡柚的售价为多少元时,当月的销售利润最大?最大利润是多少元?24. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,DE是△ABC的中位线,点F是BC边上的一个动点,连结AF交BD于点H,交DE于点G。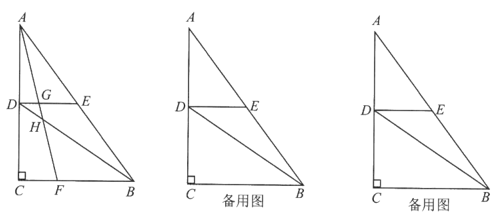 (1)、求△BDE的面积;(2)、当四边形DCFH与四边形BEGH的面积相等时,求 的值;(3)、以点F为圆心,FB为半径作⊙F,当 的值满足什么条件时,⊙F与线段DE有且只有一个交点。
(1)、求△BDE的面积;(2)、当四边形DCFH与四边形BEGH的面积相等时,求 的值;(3)、以点F为圆心,FB为半径作⊙F,当 的值满足什么条件时,⊙F与线段DE有且只有一个交点。