河南省驻马店市汝南县2020年数学中考一模试卷
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题
-
1. 在实数-3, ,0,-1中,最小的数是( )A、-3 B、0 C、-1 D、2. 如图是我国几家银行的标志,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2019年1月至8月,某市汽车产量为80万辆,其中80万用科学记数法表示为( )A、 8×104 B、0.8×105 C、8×106 D、8×1054. 如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )
3. 2019年1月至8月,某市汽车产量为80万辆,其中80万用科学记数法表示为( )A、 8×104 B、0.8×105 C、8×106 D、8×1054. 如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )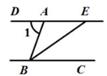 A、20° B、35° C、55° D、70°5. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( )
A、20° B、35° C、55° D、70°5. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( ) A、
A、 B、
B、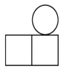 C、
C、 D、
D、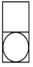 6. 一元二次方程(x+3)(x﹣3)=2x﹣5的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,以下说法中错误的是( )
6. 一元二次方程(x+3)(x﹣3)=2x﹣5的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,以下说法中错误的是( )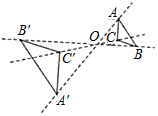 A、 · B、点C、点O、点 三点在同一直线上 C、 D、8. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).
A、 · B、点C、点O、点 三点在同一直线上 C、 D、8. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).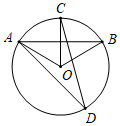 A、30° B、40° C、50° D、60°9. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )
A、30° B、40° C、50° D、60°9. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )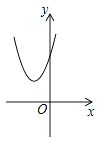 A、
A、 B、
B、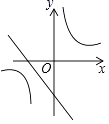 C、
C、 D、
D、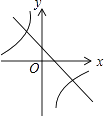 10. 如图, 为等边三角形,点 从A出发,沿 作匀速运动,则线段 的长度y与运动时间x之间的函数关系大致是( )
10. 如图, 为等边三角形,点 从A出发,沿 作匀速运动,则线段 的长度y与运动时间x之间的函数关系大致是( ) A、
A、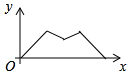 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球号之和大于5的概率为.12. 设A(x1 , y1),B(x2 , y2)是反比例函数y=﹣ 图象上的两点,若x1<x2<0,则y1与y2之间的关系是 .13. 一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积是
 14. 如图所示,四边形OABC为菱形, ,以点O为圆心,OA长为半径画弧AE,弧AE恰好经过点B,连结OE, ,则图中阴影部分的面积为.
14. 如图所示,四边形OABC为菱形, ,以点O为圆心,OA长为半径画弧AE,弧AE恰好经过点B,连结OE, ,则图中阴影部分的面积为. 15. 如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为.
15. 如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为.
三、解答题
-
16. 先化简再求值 ,其中x=3tan30°-4cos60°.17. 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D为圆心,D长为半径作作⊙D.
 (1)、求证:AC是⊙D的切线.(2)、设AC与⊙D切于点E,DB=1,连接DE,BF,EF.
(1)、求证:AC是⊙D的切线.(2)、设AC与⊙D切于点E,DB=1,连接DE,BF,EF.①当∠BAD=时,四边形BDEF为菱形;
②当AB= 时,△CDE为等腰三角形.
18. 如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据: , ,精确到0.1m.)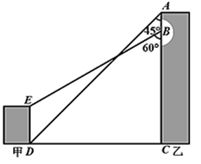 19. 如图,点A( ,4),B(3,m)是直线AB与反比例函数 (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
19. 如图,点A( ,4),B(3,m)是直线AB与反比例函数 (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC. (1)、求直线AB的表达式;(2)、△ABC和△ABD的面积分别为S1 , S2 , 求S2-S1.20. 某商场的运动服装专柜,对 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
(1)、求直线AB的表达式;(2)、△ABC和△ABD的面积分别为S1 , S2 , 求S2-S1.20. 某商场的运动服装专柜,对 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.第一次
第二次
品牌运动服装数/件
20
30
品牌运动服装数/件
30
40
累计采购款/元
10200
14400
(1)、问 两种品牌运动服的进货单价各是多少元?(2)、由于 品牌运动服的销量明显好于 品牌,商家决定采购 品牌的件数比 品牌件数的 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件 品牌运动服?21. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:x
…
0
1
2
3
…
y
…
1
2
1
0
1
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
 (1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;(2)、研究函数并结合图象与表格,回答下列问题:
(1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;(2)、研究函数并结合图象与表格,回答下列问题:①点 , , , 在函数图象上, , ;(填“>”,“=”或“<”)
②当函数值 时,求自变量x的值;
③在直线 的右侧的函数图象上有两个不同的点 , ,且 ,求 的值;
④若直线 与函数图象有三个不同的交点,求a的取值范围.
22. 如图1,在 中, , , ,点 , 分别是边 , 的中点,连接 .将 绕点 按顺时针方向旋转,记旋转角为 . (1)、问题发现
(1)、问题发现①当 时, ;②当 时, .
(2)、拓展探究试判断:当 时, 的大小有无变化?请仅就图2的情况给出证明.
(3)、问题解决当 旋转至A、B、E三点共线时,直接写出线段 的长.
23. 如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C. (1)、求抛物线的解析式;(2)、若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)、P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)、P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.