河南省许昌市2020年数学中考一模试卷
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、 B、6 C、 D、2. 新冠肺炎疫情期间,粮食安全问题受到许多国家的重视.据新华社报道,我国粮食总产量连续5年稳定在6500亿公斤以上,粮食储备充足,口粮绝对安全.将数据“6500亿”用科学记数法表示为( )A、65×1011 B、6.5×1011 C、65×1012 D、6.5×10123. 如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
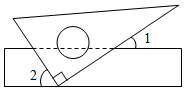 A、35° B、45° C、55° D、65°4. 下面计算正确的是( )A、3a﹣2a=1 B、2a2+4a2=6a4 C、(x3)2=x5 D、x8÷x2=x65. 桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )
A、35° B、45° C、55° D、65°4. 下面计算正确的是( )A、3a﹣2a=1 B、2a2+4a2=6a4 C、(x3)2=x5 D、x8÷x2=x65. 桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )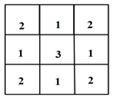 A、
A、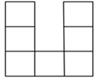 B、
B、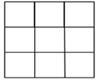 C、
C、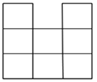 D、
D、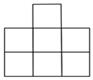 6. 不等式组 的解集在数轴上表示正确的是( )A、
6. 不等式组 的解集在数轴上表示正确的是( )A、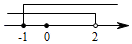 B、
B、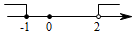 C、
C、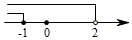 D、
D、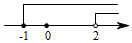 7. 九年级一班同学根据兴趣分成 A,B,C,D,E 五个小组,把各小组 人数分布绘制成如图所示的不完整统计图.则 D 小组的人数是( )
7. 九年级一班同学根据兴趣分成 A,B,C,D,E 五个小组,把各小组 人数分布绘制成如图所示的不完整统计图.则 D 小组的人数是( ) A、10 人 B、l1 人 C、12 人 D、15 人8. 在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是 ( )
A、10 人 B、l1 人 C、12 人 D、15 人8. 在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是 ( )
A、0,-4 B、0,-3 C、-3,-4 D、0,09. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为12,∠C=60°,则四边形ABEF的面积是( ) A、9 B、12 C、 D、610. 如图,在正方形ABCD中,顶点A(﹣1,0),C(1,2),点F是BC的中点,CD与y轴交于点E,AF与BE交于点G.将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第99次旋转结束时,点G的坐标为( )
A、9 B、12 C、 D、610. 如图,在正方形ABCD中,顶点A(﹣1,0),C(1,2),点F是BC的中点,CD与y轴交于点E,AF与BE交于点G.将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第99次旋转结束时,点G的坐标为( ) A、( , ) B、(﹣ , ) C、(﹣ , ) D、( ,﹣ )
A、( , ) B、(﹣ , ) C、(﹣ , ) D、( ,﹣ )二、填空题
-
11. 计算: .12. 方程 的解是.13. 在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛,恰好选中甲、乙两位同学的概率为.14. 如图,在扇形OAB中,∠AOB=90°,C是OA的中点,D是 的中点,连接CD、CB.若OA=2,则阴影部分的面积为.(结果保留π)
 15. 如图,在△ABC中,AB=AC= ,∠B=30°,D是BC上一点,连接AD,把△ABD沿直线AD折叠,点B落在B′处,连接B'C,若△AB'C是直角三角形,则BD的长为.
15. 如图,在△ABC中,AB=AC= ,∠B=30°,D是BC上一点,连接AD,把△ABD沿直线AD折叠,点B落在B′处,连接B'C,若△AB'C是直角三角形,则BD的长为.
三、解答题
-
16. 先化简,再求值: ,其中x、y满足 =2.17. 为普及防治新型冠状病毒感染的科学知识和有效方法,不断增强同学们的自我保护意识,学校举办了新型冠状病毒疫情防控网络知识竞答活动,试卷题目共10题,每题10分.现分别从七年级的三个班中各随机取10名同学的成绩(单位:分),收集数据如表:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数
人数
班级
60
70
80
90
100
1班
0
1
6
2
1
2班
1
1
3
a
1
3班
1
1
4
2
2
分析数据:
平均数
中位数
众数
1班
83
80
80
2班
83
c
d
3班
b
80
80
根据以上信息回答下列问题:
(1)、请直接写出表格中a,b,c,d的值;(2)、比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;(3)、为了让同学们重视疫情防控知识的学习,学校将给竞答成绩满分的同学颁发奖状,该校七年级新生共600人,试估计需要准备多少张奖状?18. 如图,AB是半圆O的直径,C是半圆O上一点(不与点A、B重合),D是 的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F. (1)、求证:∠FCD=∠ADE;(2)、填空:
(1)、求证:∠FCD=∠ADE;(2)、填空:①当∠FCD的度数为时,四边形OADC是菱形;
②若AB=2 ,当CF∥AB时,DF的长为.
19. 数学兴趣小组想测量河对岸两颗大树C、D之间的距离.如图所示,在河岸A点测得大树C位于正北方向上,大树D位于北偏东42°方向上.再沿河岸向东前进100米到达B处,测得大树D位于北偏东31°方向上.求两颗大树C、D之间的距离.(结果精确到1米.参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60,sin42°≈0.67,coo42°≈0.74,tan42°≈0.90).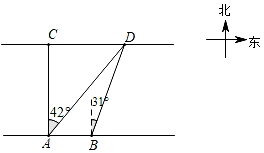 20. 某商场销售A、B两种型号的电风扇,进价及售价如表:
20. 某商场销售A、B两种型号的电风扇,进价及售价如表:品牌
A
B
进价(元/台)
120
180
售价(元/台)
150
240
(1)、该商场4月份用21000元购进A、B两种型号的电风扇,全部售完后获利6000元,求商场4月份购进A、B两种型号电风扇的数量;(2)、该商场5月份计划用不超过42000元购进A、B两种型号电风扇共300台,且B种型号的电风扇不少于50台;销售时准备A种型号的电风扇价格不变,B种型号的电风扇打9折销售.那么商场如何进货才能使利润最大?21. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数,下面我们参照学习函数的过程与方法,探究分段函数y= 的图象与性质,探究过程如下,请补充完整.(1)、列表:x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
3
m
1
0
1
2
1
n
…
其中,m= , n=.
(2)、描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.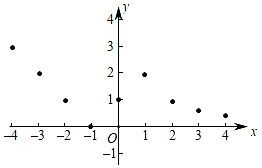 (3)、研究函数并结合图象与表格,回答下列问题:
(3)、研究函数并结合图象与表格,回答下列问题:①点A( ,y1),B(5,y2),C(x1 , ),D(x2 , 6)在函数图象上,则y1 ▲ y2 , x1 ▲ x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)、若直线y=﹣x+b与函数图象有且只有一个交点,请直接写出b的取值范围.22.(1)、发现如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.

填空:
①∠DCE的度数是;
②线段CA、CE、CD之间的数量关系是.
(2)、探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)、应用如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.
23. 如图,直线y=﹣2x+c交x轴于点A(3,0),交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B. (1)、求抛物线的解析式;(2)、点M(m,0)是线段OA上一动点(点M不与点O,A重合),过点M作y轴的平行线,交直线AB于点P,交抛物线于点N,若NP= AP,求m的值;(3)、若抛物线上存在点Q,使∠QBA=45°,请直接写出相应的点Q的坐标.
(1)、求抛物线的解析式;(2)、点M(m,0)是线段OA上一动点(点M不与点O,A重合),过点M作y轴的平行线,交直线AB于点P,交抛物线于点N,若NP= AP,求m的值;(3)、若抛物线上存在点Q,使∠QBA=45°,请直接写出相应的点Q的坐标.