河南省洛阳市伊滨区2020年数学中考三模试卷
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 据统计截至目前我国外汇储备规模为30988亿美元.将30988亿用科学记数法表示为( )A、30988×108 B、3.0988×1011 C、3.0988×1012 D、3.0988×10133. 有4个相同的立方体搭成的几何体如图所示,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 某学校在八年级开设了光影纸雕、乡土历史、兰亭书院三门校本课程,若小波和小春两名同学每人随机选择其中一门课程,则小波和小春选到同一课程的概率是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示为( )A、
4. 某学校在八年级开设了光影纸雕、乡土历史、兰亭书院三门校本课程,若小波和小春两名同学每人随机选择其中一门课程,则小波和小春选到同一课程的概率是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示为( )A、 B、
B、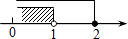 C、
C、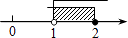 D、
D、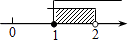 6. 如图,△ABC的顶点均在⊙O上,若∠A=36°,则∠BOC的度数为( )
6. 如图,△ABC的顶点均在⊙O上,若∠A=36°,则∠BOC的度数为( )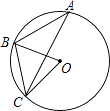 A、18° B、36° C、60° D、72°7. 若一次函数y=kx+b的图象经过一、二、四象限,则一次函数y=-bx+k的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. “绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、9. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )
A、18° B、36° C、60° D、72°7. 若一次函数y=kx+b的图象经过一、二、四象限,则一次函数y=-bx+k的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. “绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、9. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )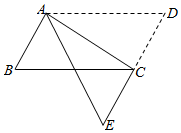 A、12 B、15 C、18 D、2110. 如图,顶角为 的等腰三角形,其底边与腰之比等k,这样的三角形称为黄金三角形,已知腰AB=1, 为第一个黄金三角形, 为第二个黄金三角形, 为第三个黄金三角形以此类推,第2020个黄金三角形的周长( )
A、12 B、15 C、18 D、2110. 如图,顶角为 的等腰三角形,其底边与腰之比等k,这样的三角形称为黄金三角形,已知腰AB=1, 为第一个黄金三角形, 为第二个黄金三角形, 为第三个黄金三角形以此类推,第2020个黄金三角形的周长( ) A、 B、 C、 D、11. 计算 .12. 已知x,y满足方程组 ,则x+y的值为( )A、5 B、7 C、9 D、313. 在 中, , ,则 .
A、 B、 C、 D、11. 计算 .12. 已知x,y满足方程组 ,则x+y的值为( )A、5 B、7 C、9 D、313. 在 中, , ,则 . 14. 如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是 . (结果保留π)
14. 如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是 . (结果保留π)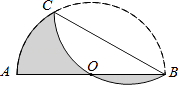 15. 如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为.
15. 如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为.
二、解答题
-
16. 先化简,再求值: ,其中 .17. 某校响应国家号召,鼓励学生积极参与体育锻炼.为了解学生一星期参与体育锻炼的时间情况,从全校2000名学生中,随机抽取50名学生进行调查,按参与体育锻炼的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
 (1)、样本中E类学生有 ▲ 人,补全条形统计图;(2)、估计全校的D类学生有人;(3)、从该样本参与体育锻炼时间在0≤t≤4的学生中任选2人,求这2人参与体育锻炼时间都在2<t≤4中的概率.18. 已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.(1)、求证:方程总有两个不相等的实数根;(2)、当p=2时,求该方程的根.19. 如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7, ≈1.7, ≈1.4)
(1)、样本中E类学生有 ▲ 人,补全条形统计图;(2)、估计全校的D类学生有人;(3)、从该样本参与体育锻炼时间在0≤t≤4的学生中任选2人,求这2人参与体育锻炼时间都在2<t≤4中的概率.18. 已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.(1)、求证:方程总有两个不相等的实数根;(2)、当p=2时,求该方程的根.19. 如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7, ≈1.7, ≈1.4) 20. 如图,双曲线 与直线 相交于 ,点P是x轴上一动点.
20. 如图,双曲线 与直线 相交于 ,点P是x轴上一动点.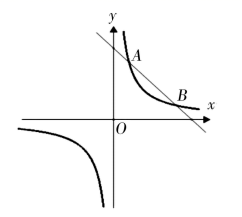 (1)、求双曲线 与直线 的解析式;(2)、当 时,直接写出x的取值范围;(3)、当 是等腰三角形时,求点P的坐标.21. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.22.(1)、问题发现
(1)、求双曲线 与直线 的解析式;(2)、当 时,直接写出x的取值范围;(3)、当 是等腰三角形时,求点P的坐标.21. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.22.(1)、问题发现如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
填空:① 的度数是;②线段AD,BE之间的数量关系为;
(2)、类比探究如图2,△ABC和△CDE均为等腰直角三角形, , , ,直线AD和直线BE交于点F.请判断 的度数及线段AD,BE之间的数量关系,并说明理由.
 (3)、解决问题
(3)、解决问题如图3,在△ABC中, , , ,点D在AB边上, 于点E, ,将△ADE绕着点A在平面内旋转,请直接写出直线DE经过点B时,点C到直线DE的距离.
 23. 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
23. 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.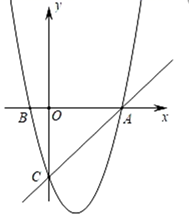 (1)、b= , c= , 点B的坐标为;(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、是否存在点P使得∠PCA=15°,若存在,请直接写出点P的横坐标.若不存在,请说明理由.
(1)、b= , c= , 点B的坐标为;(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、是否存在点P使得∠PCA=15°,若存在,请直接写出点P的横坐标.若不存在,请说明理由.