贵州省铜仁市松桃县2020年数学中考模拟试卷（4月）

试卷更新日期：2020-07-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 4的平方根（）

A、 2 B、 $- 2$ C、 $\pm \sqrt{2}$ D、 $\pm 2$

查看试题解析
2. 肥皂泡的泡壁厚度大约是0.0007mm，0.0007用科学记数法表示为（　　）

A、0.7×10^﹣³ B、7×10^﹣³ C、7×10^﹣⁴ D、7×10^﹣⁵

查看试题解析
3. 如图，直线a∥b，c是截线，∠1的度数是（　　）

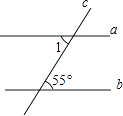A、55° B、75° C、110° D、125°

查看试题解析
4. 下列计算结果正确的是（　　）

A、2+ $\sqrt{3}$ ＝2 $\sqrt{3}$ B、 $\sqrt{8} \div \sqrt{2}$ ＝2 C、（﹣2a²）³＝﹣6a⁶ D、（a+1）²＝a²+1

查看试题解析
5. 如图是由一个圆柱体和一个长方体组成的几何体，其左视图是（）

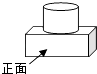A、 B、 C、 D、

查看试题解析
6. 已知下列命题：①若a＞b，则a²＞b²；②若a＞1，则（a﹣1）⁰=1；③两个全等的三角形的面积相等；④四条边相等的四边形是菱形．其中原命题与逆命题均为真命题的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 把抛物线y=﹣x²向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）

A、y=﹣（x﹣1）²﹣3 B、y=﹣（x+1）²﹣3 C、y=﹣（x﹣1）²+3 D、y=﹣（x+1）²+3

查看试题解析
8. 我国古代名著《九章算术》中有一题“今有凫起南海，七日至北海；雁起北海，九日至南海.今凫雁俱起，问何日相逢？”（凫：野鸭）设野鸭与大雁从北海和南海同时起飞，经过x天相遇，可列方程为（　　）

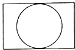A、（9﹣7）x=1 B、（9+7）x=1 C、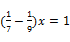 D、

查看试题解析
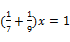9. 如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△_DOE：S_△_COA＝1：25，则S_△_DOE与S_△_COE的比是（　　）

A、1：25 B、1：5 C、1：4 D、1：3

查看试题解析
10. 平面直角坐标系中，已知A（2，2）、B（4，0）．若在坐标轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. 因式分解：ax﹣ay=

查看试题解析
12. 分式方程 $\frac{1}{x - 1}$ +1＝0的解是.

查看试题解析
13. 在函数y＝ $\frac{2}{2 x - 1}$ 中，自变量x的取值范围是.

查看试题解析
14.
对一个实数x按如图所示的程序进行操作，规定：程序运行从“输入一个实数x”到“结果是否大于88？”为一次操作．如果操作只进行一次就停止，则x的取值范围是．

查看试题解析
15. 如图，AD和CB相交于点E，BE=DE，请添加一个条件，使△ABE≌△CDE（只添一个即可），你所添加的条件是.

查看试题解析
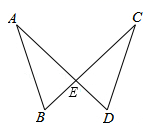16. 若关于x的一元二次方程x²﹣2x+k=0无实数根，则实数k的取值范围是．

查看试题解析
17. 从﹣1，0，1，2这四个数中，任取两个不同的数作为点的坐标，则该点在第一象限的概率为.

查看试题解析
18. 一列数a₁ ， a₂ ， a₃ ， …满足条件：a₁＝ $\frac{1}{2}$ ，a_n＝ $\frac{1}{1 - a_{n - 1}}$ （n≥2，且n为整数），则a₂₀₂₀＝.

查看试题解析

三、解答题

19.

(1)、计算：（ $\frac{1}{2020}$ ）^﹣¹+（π﹣3.14）⁰﹣6sin60°+|1﹣3 $\sqrt{3}$ |；

(2)、解方程：x²+4x﹣1＝0.

查看试题解析
20.
下列3×3网格图都是由9个相同的小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：

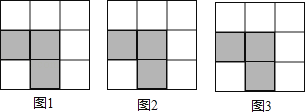(1)、选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形．

(2)、选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形．

(3)、选取2个涂上阴影，使5个阴影小正方形组成一个轴对称图形．
（请将三个小题依次作答在图1、图2、图3中，均只需画出符合条件的一种情形）

查看试题解析
21. 在校园文化艺术节中，九年级一班有1名男生和2名女生获得美术奖，另有2名男生和2名女生获得音乐奖．

(1)、从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，求刚好是男生的概率；

(2)、分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，用列表或树状图求刚好是一男生一女生的概率．

查看试题解析
22.
如图，△ABC≌△ABD，点E在边AB上，CE∥BD，连接DE．求证：

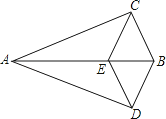(1)、∠CEB=∠CBE；

(2)、四边形BCED是菱形

查看试题解析
23.
小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500m，如图是小明和爸爸所走的路程s（m）与步行时间t（min）的函数图象．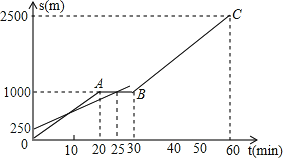

(1)、直接写出小明所走路程s与时间t的函数关系式；

(2)、小明出发多少时间与爸爸第三次相遇？

(3)、在速度都不变的情况下，小明希望比爸爸早20min到达公园，则小明在步行过程中停留的时间需作怎样的调整？

查看试题解析
24.
如图，四边形ABCD内接于⊙O，对角线AC为⊙O的直径，过点C作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF．

(1)、求∠CDE的度数；

(2)、求证：DF是⊙O的切线；

(3)、若AC=2 $\sqrt{5}$ DE，求tan∠ABD的值．

查看试题解析
25.
如图，抛物线y=ax²+bx+c（a、b、c为常数，a≠0）经过点A（﹣1，0），B（5，﹣6），C（6，0）．

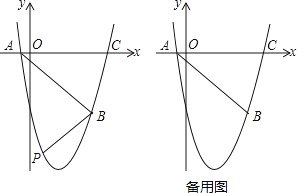(1)、求抛物线的解析式；

(2)、如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标．

查看试题解析