贵州省铜仁市2020年数学中考一模试卷
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题
-
1. (﹣1)2020等于( )A、﹣2020 B、2020 C、﹣1 D、12. 下列计算正确的是( )A、(﹣2a2)4=8a8 B、a3+a=a4 C、a5÷a2=a3 D、(a+b)2=a2+b23. 已知反比例函数y= (k≠0)的图象位于二、四象限,则一次函数y=x+k图象大致是( )A、
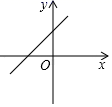 B、
B、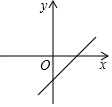 C、
C、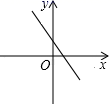 D、
D、 4. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为 ,则△ABC与△DEF对应中线的比为( )A、 B、 C、 D、5. 如图,点A、B、C是⊙0上的三点,若∠OBC=50°,则∠A的度数是( )
4. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为 ,则△ABC与△DEF对应中线的比为( )A、 B、 C、 D、5. 如图,点A、B、C是⊙0上的三点,若∠OBC=50°,则∠A的度数是( ) A、40° B、50° C、80° D、100°6. 若分式 的值为0,则x的取值为( )A、x≠1 B、x≠﹣1 C、x=1 D、x=﹣17. 某公司10名职工的5月份工资统计如下,该公司10名职工5月份工资的众数和中位数分别是( )
A、40° B、50° C、80° D、100°6. 若分式 的值为0,则x的取值为( )A、x≠1 B、x≠﹣1 C、x=1 D、x=﹣17. 某公司10名职工的5月份工资统计如下,该公司10名职工5月份工资的众数和中位数分别是( )工资(元)
2000
2200
2400
2600
人数(人)
1
3
4
2
A、2400元、2400元 B、2400元、2300元 C、2200元、2200元 D、2200元、2300元8. 已知等边三角形的周长为6,则它的内切圆和外接圆组成的圆环面积为( )A、6π B、3π C、π D、2π9. 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )A、 B、 C、 D、10. 如图已知点A(1,4),B(2,2)是反比例函数y= 的图象上的两点,动点P(x,0)在x轴上运动,当线段AP=BP时,点P的坐标是( ) A、(﹣ ,0) B、(﹣ ,0) C、( ,0) D、( ,0)
A、(﹣ ,0) B、(﹣ ,0) C、( ,0) D、( ,0)二、填空题
-
11. 世界文化遗产长城总长约6 700 00 m,用科学记数法可表示为m.12. 因式分解:a4﹣2a3+a2=.13. 菱形的两条对角线长分别是方程 的两实根,则菱形的面积为 .14. 四边形ABCD是某个圆的内接四边形,若∠A=100°,则∠C= .
15. 现定义运算“☆”,对于任意实数a、b,都有a☆b=a2﹣3a+b,若x☆2=6,则实数x的值是.16. 一个不透明的袋子中装有形状、大小均相同的3个红球,2个白球,1个黑球,从袋中随机摸出一个球是红球的概率为.17. 如图,点D在ΔABC的边BC上,∠C+∠BAD=∠DAC,tan∠BAD= ,AD= ,CD=13,则线段AC的长为.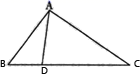 18. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…通过观察,用所发现的规律确定22016的个位数字是.
18. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…通过观察,用所发现的规律确定22016的个位数字是.三、解答题
-
19.(1)、计算:(π﹣2016)0+6cos45°﹣|﹣ |+( )﹣2(2)、先化简,再求值:( )÷ ,其中x= .20. 铜仁市教育局为了了解七年级学生寒假参加社会实践活动的天数,随机抽查本市部分七年级学生寒假参加社会实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
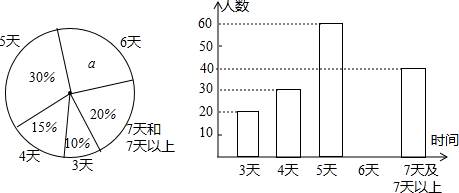 (1)、a= ▲ %,并写出该扇形所对圆心角的度数为 ▲ ;补全条形图;(2)、在这次抽样调查中,一共调查了多少名学生?(3)、如果该市有七年级学生20000人,请你估计“活动时间不少于5天”的大约有多少人?21. 已知:如图,AB=CD,BC=DA,求证:∠A=∠C.
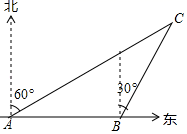
(1)、a= ▲ %,并写出该扇形所对圆心角的度数为 ▲ ;补全条形图;(2)、在这次抽样调查中,一共调查了多少名学生?(3)、如果该市有七年级学生20000人,请你估计“活动时间不少于5天”的大约有多少人?21. 已知:如图,AB=CD,BC=DA,求证:∠A=∠C.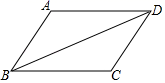 22. 如图,一艘渔船以60海里每小时的速度向正东方向航行.在A处测得灯塔C在北偏东60°方向上;继续航行1小时到达B处,此时测得灯塔C在北偏东30°方向上.已知在灯塔C周围50海里范围内有暗礁,问这艘渔船继续向东航行有无触礁的危险?
22. 如图,一艘渔船以60海里每小时的速度向正东方向航行.在A处测得灯塔C在北偏东60°方向上;继续航行1小时到达B处,此时测得灯塔C在北偏东30°方向上.已知在灯塔C周围50海里范围内有暗礁,问这艘渔船继续向东航行有无触礁的危险?