贵州省毕节市2020年数学中考模拟试卷(4月)
试卷更新日期:2020-07-21 类型:中考模拟
一、选择题
-
1. 一个数的相反数是它本身,则这个数为( )A、0 B、1 C、﹣1 D、±12.
下列四个立体图形中,左视图为矩形的是( )
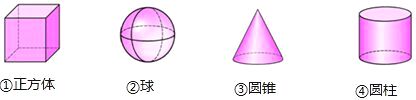 A、①③ B、①④ C、②③ D、③④3. 舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )A、4.995×1011 B、49.95×1010 C、0.4995×1011 D、4.995×10104. 下列计算正确的是( )A、a+2a2=3a2 B、a8÷a2=a4 C、a3·a2=a6 D、(a3)2=a65. 如图,P是∠ABC内一点,点Q在BC上,过点P画直线a∥BC,过点Q画直线b∥AB,若∠ABC=115°,则直线a与b相交所成的锐角的度数为( )
A、①③ B、①④ C、②③ D、③④3. 舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )A、4.995×1011 B、49.95×1010 C、0.4995×1011 D、4.995×10104. 下列计算正确的是( )A、a+2a2=3a2 B、a8÷a2=a4 C、a3·a2=a6 D、(a3)2=a65. 如图,P是∠ABC内一点,点Q在BC上,过点P画直线a∥BC,过点Q画直线b∥AB,若∠ABC=115°,则直线a与b相交所成的锐角的度数为( ) A、25° B、45° C、65° D、85°6. 点A(x1 , y1)、B(x2 , y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )A、y1 =y2 B、y1 <y2 C、y1 >y2 D、y1 ≥y27. 已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )A、 B、 C、 D、8. 某学校七年级1班统计了全班同学在1~8月份的课外阅读数量(单位:本),绘制了右边的折线统计图,下列说法正确的是( )
A、25° B、45° C、65° D、85°6. 点A(x1 , y1)、B(x2 , y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )A、y1 =y2 B、y1 <y2 C、y1 >y2 D、y1 ≥y27. 已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )A、 B、 C、 D、8. 某学校七年级1班统计了全班同学在1~8月份的课外阅读数量(单位:本),绘制了右边的折线统计图,下列说法正确的是( ) A、极差是47 B、中位数是58 C、众数是42 D、极差大于平均数9. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=
A、极差是47 B、中位数是58 C、众数是42 D、极差大于平均数9. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE= BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )  A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系xOy中,点A的坐标是(-2,0),点B的坐标是(0,6),将线段AB绕点B逆时针旋转90°后得到线段A'B.若反比例函数y= 的图象恰好经过A'点,则k的值是( )A、9 B、12 C、15 D、2411. 如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )
A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系xOy中,点A的坐标是(-2,0),点B的坐标是(0,6),将线段AB绕点B逆时针旋转90°后得到线段A'B.若反比例函数y= 的图象恰好经过A'点,则k的值是( )A、9 B、12 C、15 D、2411. 如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )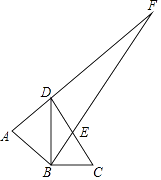 A、30° B、15° C、45° D、25°12. 如图,半径为5的⊙O中,CD是⊙O的直径,弦AB⊥CD于E,AB=8,F是 上一点,连接AF,DF,则tan∠F的值为( )
A、30° B、15° C、45° D、25°12. 如图,半径为5的⊙O中,CD是⊙O的直径,弦AB⊥CD于E,AB=8,F是 上一点,连接AF,DF,则tan∠F的值为( )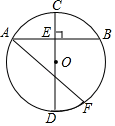 A、 B、 C、 D、213. A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/小时,乙车速度为80千米/小时,经过t小时两车相距50千米.则t的值是( )A、2 B、2或2.25 C、2.5 D、2或2.514. 抛物线y=–x2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表所示:
A、 B、 C、 D、213. A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/小时,乙车速度为80千米/小时,经过t小时两车相距50千米.则t的值是( )A、2 B、2或2.25 C、2.5 D、2或2.514. 抛物线y=–x2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表所示:x
…
–2
–1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法错误的是
A、抛物线与x轴的一个交点坐标为(–2,0) B、抛物线与y轴的交点坐标为(0,6) C、抛物线的对称轴是直线x=0 D、抛物线在对称轴左侧部分是上升的15. 如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为( )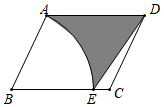 A、9 ﹣ B、9﹣ C、9 D、9﹣
A、9 ﹣ B、9﹣ C、9 D、9﹣二、填空题
-
16. 因式分解:ab2﹣2ab+a= .17. 已知一元二次方程 的两个实数根分别为 , .则抛物线 与x轴的交点坐标为.18. 二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是.
 19. 如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F两点,若AB=2EF,则k的值是.
19. 如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F两点,若AB=2EF,则k的值是.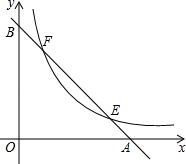 20. 已知菱形
20. 已知菱形 在平面直角坐标系的位置如图所示,
在平面直角坐标系的位置如图所示,  ,
,  ,
,  ,点
,点  是对角线
是对角线  上的一个动点,
上的一个动点,  ,当
,当  周长最小时,点
周长最小时,点  的坐标为.
的坐标为. 
三、解答题
-
21. 计算:22. 先化简,再求值: ,其中 .23. 今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
 (1)、本次抽样调查的养殖户的总户数是 ▲ ;把图2条形统计图补充完整.(2)、若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?(3)、某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.24. 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)、本次抽样调查的养殖户的总户数是 ▲ ;把图2条形统计图补充完整.(2)、若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?(3)、某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.24. 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点. (1)、求证:△BAE≌△BCF(2)、若∠ABC=50°,则当∠EBA=°时,四边形BFDE是正方形.25. 已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)、求证:△BAE≌△BCF(2)、若∠ABC=50°,则当∠EBA=°时,四边形BFDE是正方形.25. 已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题: (1)、甲骑车的速度是km/min;(2)、若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;(3)、乙在第几分钟到达B地?(4)、两人在整个行驶过程中,何时相距0.2km?26. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.
(1)、甲骑车的速度是km/min;(2)、若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;(3)、乙在第几分钟到达B地?(4)、两人在整个行驶过程中,何时相距0.2km?26. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.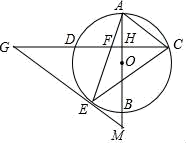 (1)、求证:EG是⊙O的切线;(2)、延长AB交GE的延长线于点M,若AH=3,CH=4,求EM的值.27. 在平面直角坐标系xOy中(如图),已知经过点A(﹣3,0)的抛物线y=ax2+2ax﹣3与y轴交于点C,点B与点A关于该抛物线的对称轴对称,D为该抛物线的顶点.
(1)、求证:EG是⊙O的切线;(2)、延长AB交GE的延长线于点M,若AH=3,CH=4,求EM的值.27. 在平面直角坐标系xOy中(如图),已知经过点A(﹣3,0)的抛物线y=ax2+2ax﹣3与y轴交于点C,点B与点A关于该抛物线的对称轴对称,D为该抛物线的顶点. (1)、直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标;(2)、联结AD、DC、CB,求四边形ABCD的面积;(3)、联结AC.如果点E在该抛物线上,过点E作x轴的垂线,垂足为H,线段EH交线段AC于点F.当EF=2FH时,求点E的坐标.
(1)、直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标;(2)、联结AD、DC、CB,求四边形ABCD的面积;(3)、联结AC.如果点E在该抛物线上,过点E作x轴的垂线,垂足为H,线段EH交线段AC于点F.当EF=2FH时,求点E的坐标.