浙江省桐乡市、海宁市2020年数学中考一模试卷
试卷更新日期：2020-07-21 类型：中考模拟
一、选择题（本题有10小题，每题3分，共30分．请选出各题中唯一的正确选项，不选、多选、错选，均不得分）
-
1. -2020的绝对值是（ ）A、2020 B、-2020 C、 D、2. 计算a3·（-a）的结果是（ ）A、a² B、-a² C、a4 D、-a43. 不等式2x+9≥3（x+2）的解集是（ ）A、x≥3 B、x≥7 C、x≤3 D、x≤74. 下列等式从左边到右边的变形中，是因式分解的是（ ）A、a（a+3）=a2+3a B、a2+4a-5=a（a+4）-5 C、（a+2）（a-2）=a2-4 D、a2+6a+9=（a+3）25. 如图，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列说法正确的是（ ）
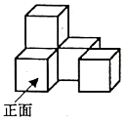A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是36. 如图是某校学生到校方式的扇形统计图．若该校骑自行车到校的学生有200人，则步行到校的学生有（ ）
A、120人 B、160人 C、125人 D、180人7. 《九章算术》是中国古代第一部数学专著，书中有这样一题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各儿何？”大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价格是多少？设共有x个人，该物品价格是y元，则下列方程组正确的是（ ）A、 B、 C、 D、8. 在△ABC中，若一个内角等于另外两个内角的差，则（ ）A、必有一个内角等于30° B、必有一个内角等于45° C、必有一个内角等于60° D、必有一个内角等于90°9. 如图，⊙O经过菱形ABCD的顶点B，C，且与边AD相切于点E。若AE=1，ED=5，则⊙O的半径为（ ）
A、 B、 C、 D、10. 对于函数y=ax2-（2a+1）x-3a+1（a是常数），有下列说法：①函数图象与坐标轴总有三个不同的交点；
②当x<1时，不是y随x的增大而增大就是y随x的增大而减小；
③若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数。
其中错误的说法是（ ）
A、① B、①② C、②③ D、①③二、填空题（本题有6小题，每题4分，共24分）
-
11. 计算： = 。12. 若x=2y+3，则代数式3x-6y+1的值是。13. 在网络课程学习中，小蕾和小丽分别在《好玩的数学》《美学欣赏》《人文中国》中随机选择一门，两人恰好选中同一门课程的概率为。14. 如图，Rt△OAB中，∠OAB=90°，O是坐标原点，点A在x轴的正半轴上，点B在第一象限。已知OA=2，∠AOB=30°，将△OAB绕点O按逆时针方向旋转150°，得到△OA'B'，则点A的对应点A'的坐标是。
15. 如图，已知 ABCD，以B为位似中心，作 ABCD的位似图形 EBFG，位似图形与原图形的位似比为 ，连结AG，DG。若 ABCD的面积为24，则△ADG的面积为。
16. 如图，等边△ABC中，AB=2，点D是以A为圆心，半径为1的圆上一动点，连接CD，取CD的中点E，连接BE，则线段BE的最大值与最小值之和为。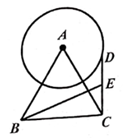
三、解答题（本题有8小题，第17~19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）
-
17. 在解答“化简： ”时，明明的解答过程如下：
1
明明的解答从第几步开始出错的？请写出正确的解答过程。
18. 如图，在△ABC中，已知AB=AC。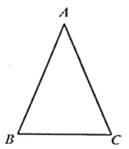
(1)、尺规作图：画△ABC的外接圆⊙O（保留作图痕迹，不写画法）。(2)、连结OB，OC，若∠A=45°，BC=6，求扇形OBC的弧长。19. 如图，反比例函数y= （k≠0）图象与一次函数y=-x+b图象相交于A（1，3），B（m，1）两点。
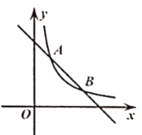(1)、求反比例函数和一次函数的表达式。(2)、已知点P（a，0）（a>0），过点P作平行于y轴的直线，在第一象限内与一次函数y=-x+b的图象相交于点M，与反比例函数y= 上的图象相交于点N。若PM>PN，结合函数图象直接写出a的取值范围。20. 如图，△ABC中，∠BAC=90，∠B=36°， AD是斜边BC上的中线，将△ACD沿AD折叠，使点C落在点F处，线段DF与AB相交于点E。
(1)、求∠BDE的度数。(2)、求证：△DEH∽△ADB。(3)、若BC=4，求BE的长。21. 某校七年级甲班、乙班举行一分钟投篮比赛，每班派10名学生参赛，在规定时间内进球数不少于8个为优秀学生。比赛数据的统计图表如下（数据不完整）：
甲班乙班每生进球个数统计图
甲班
乙班
平均数
6.5
a
中位数
b
6
方差
3.45
4.65
优秀率
30%
c
根据以上信息，解答下列问题：
(1)、直接写出a，b，c的值。(2)、你认为哪个班的比赛成绩要好一些？请简要说明理由。22. 如图1是某体育看台侧面的示意图，观众区AC的坡度i=1：2，顶端C离水平地面AB的高度为15m，顶棚外沿处的点E恰好在点A的正上方，从D处看E处的仰角α=30°，竖直的立杆上C，D两点间的距离为5m。
(1)、求观众区的水平宽度AB。(2)、求图1中点E离水平地面的高度EA。(3)、因为遮阳需要，现将顶棚ED绕D点逆时针转动11°30'，若E点在地面上的铅直投影是点F（图2） ，求AF。（sin11°30'≈0.20，cos11°30'≈0.98，tan11°30'≈0.20；sin18°30'≈0.32，cos18°30'≈0.95，tan18°30'≈0.33， 结果精确到0.1m）23. 定义：每个内角都相等的八边形叫做等角八边形。容易知道，等角八边形的内角都等于135°。下面，我们来研究它的一些性质与判定：
(1)、如图1， 等角八边形ABCDEFGH中，连结BF。①请直接写出∠ABF+∠GFB的度数。
②求证：AB∥EF。
③我们把AB与EF称为八边形的一组正对边．由②同理可得：BC与FG，CD与GH，DE与HA这三组正对边也分别平行。请模仿平行四边形性质的学习经验，用一句话概括等角八边形的这一性质。
(2)、如图2，等角八边形ABCDEFGH中，如果有AB=EF，BC=FG，则其余两组正对边CD与GH，DE与HA分别相等吗？证明你的结论。(3)、如图3，八边形ABCDEFGH中，若四组正对边分别平行，则显然有∠A=∠E，∠B=∠F，∠C=∠G，∠D=∠H。请探究：该八边形至少需要已知几个内角为135°，才能保证它一定是等角八边形？24. 受新冠疫情影响，3月1日起，“君乐买菜”网络公司某种蔬菜的销售价格开始上涨。如图1，前四周该蔬菜每周的平均销售价格y（元/kg）与周次x（x是正整数，1≤x<5）的关系可近似用函数y= x+a刻画；进入第5周后，由于外地蔬菜的上市，该蔬菜每周的平均销售价格y（元/kg）从第5周的6元/kg下降至第6周的5.6元/kg，y与周次x（5≤x≤7）的关系可近似用函数y= x2+bx+5刻画。
(1)、求a，b的值。(2)、若前五周该蔬菜的销售量m（kg）与每周的平均销售价格y（元/kg）之间的关系可近似地用如图2所示的函数图象刻画，第6周的销售量与第5周相同。①求m与y的函数表达式；
②在前六周中，哪一周的销售额w（元）最大？最大销售额是多少？
(3)、若该蔬菜第7周的销售量是100kg，由于受降雨的影响，此种蔬菜第8周的可销售量将比第7周减少n%（n>0）。为此，公司又紧急从外地调运了5此种蔬菜，刚好满足本地市民的需要，且使此种蔬菜第8周的销售价格比第1周仅上涨0.8n%。若在这一举措下，此种蔬菜在第8周的总销售额与第7周刚好持平，请通过计算估算出n的整数值。