浙江省湖州市长兴县2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-07-21 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 若式子 在实数范围内有意义,则工的取值范围是( )A、≥3 B、x≤3 C、x>3 D、x<32. 有一组数据: ,5, , , , , ,5,则这组数据的众数是( )A、 B、 C、 D、3. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=3 D、xx=0,x2=-34. 正十二边形的外角和的度数为( )A、180° B、360° C、720° D、1800°5. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
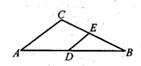 A、8 B、10 C、12. D、146. 二次根式 , , 的大小关系是( )A、 < < B、 < < C、 < < D、 < <7. 上图中信息是小明和小华射箭的成绩,两人都射了10箭,则射箭成绩的方差较大的是( )
A、8 B、10 C、12. D、146. 二次根式 , , 的大小关系是( )A、 < < B、 < < C、 < < D、 < <7. 上图中信息是小明和小华射箭的成绩,两人都射了10箭,则射箭成绩的方差较大的是( )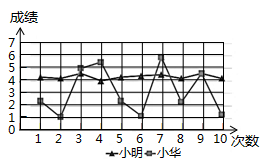 A、小明 B、小华 C、两人一样 D、无法确定8. 在菱形ABCD中,∠ABC=60°,若AB=3,则菱形ABCD的面积是( )A、 B、8 C、 D、9. 在四边形ABCD中:①AB∥CD②AD∥BC③AB=CD④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A、小明 B、小华 C、两人一样 D、无法确定8. 在菱形ABCD中,∠ABC=60°,若AB=3,则菱形ABCD的面积是( )A、 B、8 C、 D、9. 在四边形ABCD中:①AB∥CD②AD∥BC③AB=CD④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A、3种 B、4种 C、5种 D、6种10. 如图,在Rt△ABC中,∠BAC=90°,且AB=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为( )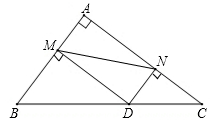 A、 B、 C、3 D、4
A、 B、 C、3 D、4二、填空题(每小题4分,共24分)
-
11. 化简: =。12. 写出一个根为1和3的一元二次方程:。13. 如图,以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是。
 14. 已知x2-2 x+1=0,则x- =。15. 如图,点P是线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,点M,N分别是对角线AC,BE的中点,连接MN,PM,PN,若∠DAP=60°,AP2+3PB2=5, 则线段MN的长为。
14. 已知x2-2 x+1=0,则x- =。15. 如图,点P是线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,点M,N分别是对角线AC,BE的中点,连接MN,PM,PN,若∠DAP=60°,AP2+3PB2=5, 则线段MN的长为。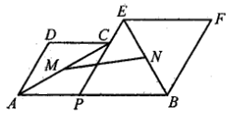
三、解答题(共66分)
-
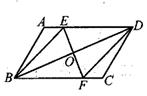
16. 计算:(1)、(2)、( +1)(2-2 )17. 解下列方程:(1)、x2-4x-5=0(2)、x2+4x=x+418. 如图,在 ABCD中,点O是对角线BD的中点,过点O任作一条直线,分别与AD,BC交于点E,F。
求证:四边形BEDF是平行四边形。
 19. 某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%,面试占40%计算候选人的综合成绩(满分为100分),他们的各项成绩如下表所示:
19. 某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%,面试占40%计算候选人的综合成绩(满分为100分),他们的各项成绩如下表所示:候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)、这四名候选人面试成绩的平均数是;(2)、现得知候选人丙的综合成绩为87.6分,则表中x的值等于;(3)、求其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选。20. 求值:(1)、已知x= ,y= ,求 的值;(2)、已知x= +1,y= -1,求2x2+3xy+2y2的值。21. ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF。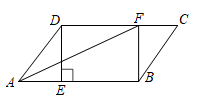 (1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE-3,DF=5,求矩形BFDE的面积。22. 宾馆有50间房供游客居住,原定价每间房每天190元,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房(物价部门规定,此类宾馆的入住费用不得超过原定价的1.5倍)。如果有游客居住,宾馆需对居住的每间房每天支出20元的费用。(1)、如果每间房当天的定价比房间住满时的房价增加x元时,宾馆间房有游客居住(用含x的代数式表示);(2)、当房价定为多少元时,宾馆当天的利润为9450元?23. 如图所示,已知正方形OEFG的顶点O为正方形ABCD对角线AC,BD的交点,连接CE,DG。
(1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE-3,DF=5,求矩形BFDE的面积。22. 宾馆有50间房供游客居住,原定价每间房每天190元,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房(物价部门规定,此类宾馆的入住费用不得超过原定价的1.5倍)。如果有游客居住,宾馆需对居住的每间房每天支出20元的费用。(1)、如果每间房当天的定价比房间住满时的房价增加x元时,宾馆间房有游客居住(用含x的代数式表示);(2)、当房价定为多少元时,宾馆当天的利润为9450元?23. 如图所示,已知正方形OEFG的顶点O为正方形ABCD对角线AC,BD的交点,连接CE,DG。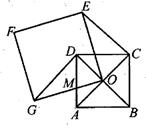 (1)、求证:△DOG≌△COE;(2)、若DG⊥BD,正方形ABCD的边长为2,线段AD与线段OG相交于点M,且∠OMD=75°,求CE的长;(3)、在(2)的条件下,把正方形OEFG绕点O旋转,直接写出点B到点F的最短距离。
(1)、求证:△DOG≌△COE;(2)、若DG⊥BD,正方形ABCD的边长为2,线段AD与线段OG相交于点M,且∠OMD=75°,求CE的长;(3)、在(2)的条件下,把正方形OEFG绕点O旋转,直接写出点B到点F的最短距离。