浙江省杭州市萧山区高桥教育集团高桥金帆2020年数学中考适应性卷

试卷更新日期：2020-07-21 类型：中考模拟

进入出卷网下载

一、仔细选一选，下面每小题给出的四个选项中，只有一个是正确的。（本题有10个小题，每小题3分，共30分）

1. 在下列实数中： $\frac{1}{2020}$ ， $\sqrt{2020}$ ，2020，0最大的数是（）

A、 $\frac{1}{2020}$ B、 $\sqrt{2020}$ C、2020 D、0

查看试题解析
2. 点M（m+1，m+3）在y轴上，则M点的坐标为（）

A、（0，-4） B、（4，0） C、（-2，0） D、（0，2）

查看试题解析
3. 如图，AD∥BE∥CF，AB=3，BC=6，DE=2，则EF的值为（）

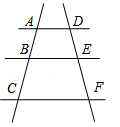A、2 B、3 C、4 D、5

查看试题解析
4. 掷一枚质地均匀的硬币6次，下列说法正确的是（）

A、必有3次正面朝上 B、可能有3次正面朝上 C、至少有1次正面朝上 D、不可能有6次正面朝上

查看试题解析
5. 一列列车自全国铁路第5次大提速后，速度提高了26千米/时，现在该列车从甲站到乙站所用的时间比原来减少了1小时，已知甲、乙两站的路程是312千米，若设列车提速前的速度是x千米/时，则根据题意所列方程正确的是（）

A、 $\frac{312}{x} - \frac{312}{x + 26} = 1$ B、 $\frac{312}{x + 26} - \frac{312}{x} = 1$ C、 $\frac{312}{x} - \frac{312}{x - 26} = 1$ D、 $\frac{312}{x - 26} - \frac{312}{x} = 1$

查看试题解析
6. 如图，在Rt△ABC中，∠ACB=90°， CD⊥AB，垂足为点D，如果 $\frac{C △_{A D C}}{C △_{C D B}} = \frac{3}{2}$ ，AD=9，那么BC的长是（）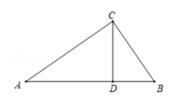

A、4 B、6 C、2 $\sqrt{13}$ D、3 $\sqrt{10}$

查看试题解析
7. 用三个不等式a>b，ab>0， $\frac{1}{a}$ > $\frac{1}{b}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题组成真命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 如图，Rt△AOB中，∠AOB=90°，顶点A，B分别在反比例函数y= $\frac{2}{x}$ （x>0）与y= $- \frac{8}{x}$ （x<0）的图象上，则下列等式成立的是（）

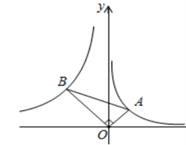A、sin∠ BAO= $\frac{\sqrt{5}}{5}$ B、cos∠BAO= $\frac{\sqrt{5}}{2}$ C、tan∠BAO=2 D、sin∠ABO= $\frac{1}{4}$

查看试题解析
9. 已知二次函数y=a（x-2）²+c，当x=x₁时，函数值为y₁；当x=x₂时，函数值为y₂ ，若|x₁-2|>|x₂-2|，则下列表达式正确的是（）

A、y₁+y₂>0 B、y₁-y₂>0 C、a（y₁-y₂）>0 D、a（y₁+y₂）>0

查看试题解析
10. 如图所示，在矩形ABCD中，F是DC上一点，AE平分∠BAF交BC于点E，且DE⊥AF，垂足为点M，BE=3，AE=2 $\sqrt{6}$ ，则MF的长是（）

A、 $\sqrt{15}$ B、 $\frac{\sqrt{15}}{10}$ C、1 D、 $\frac{\sqrt{15}}{15}$

查看试题解析

二、认真填一填（本题有6个小题，每小题4分，共24分）

11. 分解因式：ab²-4ab+4a=。

查看试题解析
12. 在一个布袋中装有只有颜色不同的a个小球，其中红球的个数为2，随机摸出一个球记下颜色后再放回袋中，通过大量重复实验后发现，摸到红球的频率稳定于0.2，那么可以推算出a大约是.

查看试题解析
13. 不等式组 ${\begin{cases} 5 x + 8 > 3 (x + 1) \\ \frac{1}{2} x - 1 < 7 - \frac{3}{2} x \end{cases}$ 的最大整数解为。

查看试题解析
14. 已知关于x的方程（k-1）x²-2kx+k-3=0有两个相等的实根，则k的值是。

查看试题解析
15. 如图，△ABC中，∠C=90°，CA=CB，D为AC上的一点，AD=3CD，AE⊥AB交BD的延长线于E，记△EAD，△DBC的面积分别为S₁ ， S₂ ，则S₁：S₂=。

查看试题解析
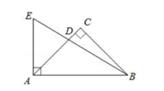16. 如图，在Rt△ABC中，ABC=90°，AB=2，BC=4，点P在边BC上，联结AP，将△ABP绕着点A旋转，使得点P与边AC的中点M重合，点B的对应点是点B'，延长AB'交BC于E，则EP的长等于。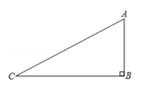

查看试题解析

三、全面答一答（本题有7个小题，共66分）解答应写出文字说明、证明过程或推演步骤，如果觉得有的题目有点困难，你们把自己能写出的解答写出一部分也可以。

17. 一个不透明的布袋里装有4个只有颜色不同的球，其中3个红球，1个白球。

(1)、从布袋中任意摸出1个球，求摸出是红球的概率；

(2)、从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率（请用“画树状图”或“列表”等方法写出分析过程）。

查看试题解析
18. 已知 ${\begin{cases} x = m - 3 ① \\ y = m - 5 ② \end{cases}$

(1)、若2x+y=-5，求m的值；

(2)、求y关于x的表达式；

(3)、若x>1，y<0，求2x+y的值的取值范围。

查看试题解析
19. 如图，在△ABC中，点D，E分别在边AB，AC上，∠AED=∠B，射线AG分别交线段DE，BC于点F，G，且 $\frac{A D}{A C} = \frac{D F}{C G}$ ．

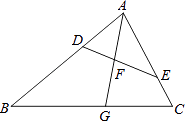(1)、求证：△ADF∽△ACG；

(2)、若 $\frac{A D}{A C} = \frac{1}{2}$ ，求 $\frac{A F}{F G}$ 的值．

查看试题解析
20. 已知一次函数y₁=3x-3的图象与反比例函数y₂= $\frac{m}{x}$ 的图象交于点A（a，3），B（-1，b）。

(1)、求a，b的值和反比例函数的表达式；

(2)、设点P（h，y₁），Q（h，y₂）分别是两函数图象上的点；
①试直接写出当y₁>y₂时h的取值范围；

②若y₂-y₁=3，试求h的值。

查看试题解析
21. 如图，△ABC是⊙O内接三角形，AC是直径，点P是⊙O外一点，PA=PB，且PA是⊙O切线。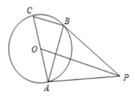

(1)、求证：PB是⊙O的切线；

(2)、若OP=8，⊙O的半径为2 $\sqrt{2}$ ，求BC的长。

查看试题解析
22. 已知点A（1，1）为函数y=ax²+bx+4（a，b为常数，且a≠0）上一点。

(1)、用a的代数式表示b；

(2)、若1≤a≤2，求 $- \frac{b}{2 a}$ 的范围；

(3)、在（2）的条件下，设当 $\frac{1}{2}$ ≤x≤2时，函数y=ax²+bx+4的最大值为m，最小值为n，求m-n（用a的代数式表示）。

查看试题解析
23. 如图，已知⊙O的半径长为1，AB、AC是⊙O的两条弦，且AB=AC，BO的延长线交AC于点D，联结OA、OC。

(1)、求证：△AOB≌△AOC；

(2)、当△OCD是直角三角形时，求B、C两点的距离；

(3)、记△AOB、△AOD、△COD的面积分别为S₁、S₂、S₃ ，如果S₂是S₁和S₃的比例中项，求OD的长。

查看试题解析

浙江省杭州市萧山区高桥教育集团高桥金帆2020年数学中考适应性卷

一、仔细选一选，下面每小题给出的四个选项中，只有一个是正确的。 （本题有10个小题，每小题3分，共30分）

二、认真填一填（本题有6个小题，每小题4分，共24分）

三、全面答一答（本题有7个小题，共66分） 解答应写出文字说明、证明过程或推演步骤，如果觉得有的题目有点困难，你们把自己能写出的解答写出一部分也可以。

一、仔细选一选，下面每小题给出的四个选项中，只有一个是正确的。（本题有10个小题，每小题3分，共30分）

三、全面答一答（本题有7个小题，共66分）解答应写出文字说明、证明过程或推演步骤，如果觉得有的题目有点困难，你们把自己能写出的解答写出一部分也可以。