2021高考一轮复习第四讲函数及其表示

试卷更新日期：2020-07-20 类型：一轮复习

进入出卷网下载

一、单选题

1. 若定义在R的奇函数f(x)在 $(- \infty ， 0)$ 单调递减，且f(2)=0，则满足 $x f (x - 1) \geq 0$ 的x的取值范围是（）

A、 $[- 1 ， 1] \cup [3 ， + \infty)$ B、 $[- 3 ， - 1] \cup [0 ， 1]$ C、 $[- 1 ， 0] \cup [1 ， + \infty)$ D、 $[- 1 ， 0] \cup [1 ， 3]$

查看试题解析
2. 已知函数 $f (x) = {\begin{array}{l} x^{3} ， & x ⩾ 0 ， \\ - x ， & x < 0. \end{array}$ 若函数 $g (x) = f (x) - | k x^{2} - 2 x | (k \in R)$ 恰有4个零点，则k的取值范围是（）

A、 $(- \infty ， - \frac{1}{2}) \cup (2 \sqrt{2} ， + \infty)$ B、 $(- \infty ， - \frac{1}{2}) \cup (0 ， 2 \sqrt{2})$ C、 $(- \infty ， 0) \cup (0 ， 2 \sqrt{2})$ D、 $(- \infty ， 0) \cup (2 \sqrt{2} ， + \infty)$

查看试题解析
3. 已知函数 $f (x) = {\begin{array}{l} \lg x ， x \geq 1 \\ - \lg (2 - x) ， x < 1 \end{array}$ ， $g (x) = x^{3}$ ，则方程 $f (x) = g (x - 1)$ 所有根的和等于（）

A、1 B、2 C、3 D、4

查看试题解析
4. 设函数 $y = f (x)$ 在R上有意义，对给定实数N，定义函数 $f_{N} (x) = {\begin{array}{l} f (x), f (x) \leq N \\ N, f (x) > N \end{array}$ ，则称函数 $f_{N} (x)$ 为 $f (x)$ 的“孪生函数”，若给定函数 $f (x) = 2 - x^{2}$ ， $N = - 1$ ，则 $y = f_{N} (x)$ 的值域为（）

A、 $[1, 2]$ B、 $[- 1, 2]$ C、 $(- \infty, 1]$ D、 $(- \infty, - 1]$

查看试题解析
5. 已知函数 $f (x) = 1 - x^{2}$ ， $g (x) = m \sin (\frac{π}{6} x) + 2 - m (m > 0)$ ，若存在 $x_{1}, x_{2} \in [0, 1]$ ，使得 $f (x_{1}) \geq g (x_{2})$ 成立，则m的取值范围是（）

A、 $(0, 1]$ B、 $[1, 4)$ C、 $[1, + \infty)$ D、 $(0, 4)$

查看试题解析
6. 已知函数 $f (x) = {\begin{cases} \log_{2} x, x > 0 \\ 3^{x}, x \leq 0 \end{cases}$ ，则 $f [f (\frac{1}{4})]$ 的值是（）

A、 $\frac{1}{4}$ B、4 C、 $\frac{1}{9}$ D、 $\sqrt{3}$

查看试题解析
7. 下列各组函数中，表示同一个函数的是（）

A、 $y = \frac{x^{2} - 1}{x - 1}$ 与 $y = x + 1$ B、 $y = 1$ 与 $y = x^{0}$ C、 $y = \sqrt{x^{2}} - 1$ 与 $y = x - 1$ D、 $y = x$ 与 $y = \log_{a} a^{x} (a > 0 且 a \neq 1)$

查看试题解析
8. 已知函数f（x+2）＝x² ，则f（x）等于（）

A、x²+2 B、x²-4x+4 C、x²-2 D、x²+4x+4

查看试题解析
9. 函数 $f (x)$ 的图象如图所示，则它的解析式可能是（）

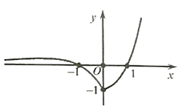A、 $f (x) = \frac{x^{2} - 1}{2^{x}}$ B、 $f (x) = 2^{x} (| x | - 1)$ C、 $f (x) = | \ln | x | |$ D、 $f (x) = x e^{x} - 1$

查看试题解析
10. 设函数 $f (x) = {\begin{array}{l} x^{2} - 2 (x \geq 2) \\ \log_{2} x (x < 2) \end{array}$ ，若 $f (m) = 7$ ，则实数m的值为（）

A、0 B、1 C、-3 D、3

查看试题解析
11. 下列与函数 $y = \frac{1}{\sqrt{x}}$ 定义域和单调性都相同的函数是（）

A、 $y = 2^{\log_{2} x}$ B、 $y = \log_{2} {(\frac{1}{2})}^{x}$ C、 $y = \log_{2} \frac{1}{x}$ D、 $y = x^{\frac{1}{4}}$

查看试题解析

二、填空题

12. 函数 $f (x) = \frac{1}{x + 1} + \ln x$ 的定义域是．

查看试题解析
13. 函数f（x）= $\sqrt{e^{x} - 1}$ 的定义域为。

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} x + 2, x \leq 0 \\ f (- x), x > 0 \end{array}$ ， $g (x) = f (x - 2)$ ，若 $g (x - 1) \geq 1$ ，则实数x的取值范围为．

查看试题解析
15. 函数 $f (x) = \sqrt{x} (\sqrt{x} - 4) + x - 1$ 的值域为.

查看试题解析
16. 已知函数 $f (x) = \log_{a} (\sqrt{x^{2} + a} - x) + b$ ，若 $f (3) - f (- 3) = - 1$ ，则实数a的值是．

查看试题解析
17. 已知函数 $f (x) = {\begin{array}{l} \ln x, x > 0 \\ {(\frac{1}{2})}^{x} - 2, x \leq 0 \end{array}$ 若 $f (f (a)) \leq 0$ ，则实数a的取值范围为．

查看试题解析
18. 已知函数f(x)= $a (\frac{2^{x} - 1}{2^{x} + 1}) + b \sqrt[{}^{3}]{x} + 2$ 其中 $a, b$ 为常数，且 $f (3) = 1$ ，则 $f (- 3) =$ .

查看试题解析

2021高考一轮复习 第四讲 函数及其表示

一、单选题

二、填空题

2021高考一轮复习第四讲函数及其表示