2020年暑期衔接训练青岛版数学八年级下册：第15讲第九章《二次根式》单元测试

试卷更新日期：2020-07-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 式子：① $\sqrt{a}$ ；② $\sqrt{π}$ ；③ $\sqrt{| 1 - x |}$ ；④ $\sqrt{x + 2}$ ；⑤ $\sqrt{- x}$ ；⑥ $\sqrt{5 x^{2} - 1}$ ；⑦ $\sqrt{a^{2} + 2}$ ⑧ $\sqrt{3 b^{2}}$ 中是二次根式的代号为（）

A、①②④⑥ B、②④⑧ C、②③⑦⑧ D、①②⑦⑧

查看试题解析
2. 若函数y＝ $\frac{\sqrt{x + 1}}{x - 1}$ ，则自变量x的取值范围是（）

A、－1＜x＜1 B、x≥－1且x≠1 C、x≥－1 D、x≠1

查看试题解析
3. 在二次根式 $\sqrt{16 x^{3}}$ ，﹣ $\frac{\sqrt{2}}{3}$ ， $\sqrt{0.5}$ ， $\sqrt{\frac{a}{x}}$ ， $\sqrt{a^{2} - b^{2}}$ 中，最简二次根式有（）个．

A、1 B、2 C、3 D、4

查看试题解析
4. 若等腰三角形的两边长分别为 $\sqrt{50}$ 和 $\sqrt{72}$ ，则这个三角形的周长为（　　）

A、 $11 \sqrt{2}$ B、 $16 \sqrt{2}$ 或 $17 \sqrt{2}$ C、 $17 \sqrt{2}$ D、 $16 \sqrt{2}$

查看试题解析
5. 已知a﹣b=2+ $\sqrt{3}$ ， b﹣c=2﹣ $\sqrt{3}$ ，则a²+b²+c²﹣ab﹣bc﹣ac的值为（　　）

A、10 $\sqrt{3}$ B、12 $\sqrt{3}$ C、10 D、15

查看试题解析
6. 若三角形的三边分别是a ， b ， c ，且 ${(a - 2 \sqrt{5})}^{2} + \sqrt{a - b - 1} + |c - 4|$ =0，则这个三角形的周长是（　　）

A、 $2 \sqrt{5} + 5$ B、 $4 \sqrt{5} - 3$ C、 $4 \sqrt{5} + 5$ D、 $4 \sqrt{5} + 3$

查看试题解析
7. 实数a在数轴上的位置如图所示，则 $\sqrt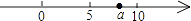{{(a - 4)}^{2}} + \sqrt{{(a - 11)}^{2}}$ 化简后为（　　）

A、7 B、−7 C、2a−15 D、无法确定

查看试题解析
8. 若 $\sqrt{x}$ + $\sqrt{\frac{1}{x}}$ = $\sqrt{6}$ ， 0＜x＜1，则 $\sqrt{x}$ ﹣ $\sqrt{\frac{1}{x}}$ =（　　）

A、- $\sqrt{2}$ B、-2 C、±2 D、± $\sqrt{2}$

查看试题解析
9. 若 $\sqrt{\frac{y + 2}{2 x - 1}} = \frac{\sqrt{y + 2}}{\sqrt{2 x - 1}}$ ，且x+y=5，则x的取值范围是（　　）

A、x＞ $\frac{1}{2}$ B、 $\frac{1}{2}$ ≤x＜5 C、 $\frac{1}{2}$ ＜x＜7 D、 $\frac{1}{2}$ ＜x≤7

查看试题解析
10. 计算： $\sqrt{{(2 a - 1)}^{2}} + \sqrt{{(1 - 2 a)}^{2}}$ 的值是（　　）

A、0 B、4a﹣2 C、2﹣4a D、2﹣4a或4a﹣2

查看试题解析
11. 若|1﹣x|=1+|x|，则 $\sqrt{{(x - 1)}^{2}}$ 等于（　　）

A、x﹣1 B、1﹣x C、1 D、-1

查看试题解析
12. 已知实数a满足 $| 2000 - a | + \sqrt{a - 2001} = a$ ，那么a﹣2000²的值是（　　）

A、1999 B、2000 C、2001 D、2002

查看试题解析

二、填空题

13. 设 $\frac{1}{3 - \sqrt{7}}$ 的整数部分是a，小数部分是b，则 $a^{2} + (1 + \sqrt{7}) a b$ 的值是．

查看试题解析
14. 如图，矩形内有两个相邻的正方形，面积分别为3和27，那么图中阴影部分的面积为。

查看试题解析
15. 已知x是实数且满足（x﹣3） $\sqrt{2 - x}$ =0，则相应的代数式x²+2x﹣1的值为．

查看试题解析
16. 已知x= $\sqrt{2011} - \sqrt{2012}$ ，y= $\sqrt{2012} - \sqrt{2013}$ ，则x与y之间的大小关系是．

查看试题解析
17. 已知 $\sqrt{x}$ ﹣ $\frac{1}{\sqrt{x}}$ =2，则 $\sqrt{x^{2} + \frac{1}{x^{2}} + 14}$ 的值为．

查看试题解析
18. 设 $a = \sqrt{7}$ ， $b = 2 + \sqrt{3}$ ， $c = \frac{1}{\sqrt{3} - \sqrt{2}}$ ，则 $a$ ， $b$ ， $c$ 从小到大的顺序是.

查看试题解析
19. 已知 $x + y = 6$ ， $x y = - 3$ 且 $x > y$ ，则 $\sqrt{- \frac{x}{y}} + \sqrt{- \frac{y}{x}} =$ ．

查看试题解析

三、解答题

20. 计算：

(1)、 $\sqrt{48} - \sqrt{27} + \sqrt{\frac{1}{3}}$

(2)、 $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}} - {(3 \sqrt{2} - 1)}^{2}$

查看试题解析
21. 若a ， b为有理数，且 $\sqrt{8} + \sqrt{18} + \sqrt{\frac{1}{8}}$ = $a + b \sqrt{2}$ ，求 $b^{a}$ 的值。

查看试题解析
22. 若最简二次根式 $\sqrt[a + 1]{2 a + 5}$ 与 $\sqrt{3 b + 4 a}$ 是同类二次根式，求a²⁰¹⁶+b²⁰¹⁶的值．

查看试题解析
23. 已知y＜ $\sqrt{x - 2}$ + $\sqrt{2 - x}$ +3，化简|y﹣3|﹣ $\sqrt{y^{2} - 8 y + 16}$ ．

查看试题解析
24. 阅读下面计算过程：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；

$\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ .

求：

(1)、 $\frac{1}{\sqrt{7} + \sqrt{6}}$ 的值.

(2)、 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （n为正整数）的值.

(3)、 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ....... + \frac{1}{\sqrt{100} + \sqrt{99}}$ 的值.

查看试题解析
25. 观察下列格式， $\frac{\sqrt{5} - 1}{2}$ - $\frac{2}{\sqrt{5} - 1}$ ， $\frac{\sqrt{8} - 2}{2} - \frac{2}{\sqrt{8} - 2}$ ， $\frac{\sqrt{13} - 3}{2} - \frac{2}{\sqrt{13} - 3}$ ， $\frac{\sqrt{20} - 4}{2} - \frac{2}{\sqrt{20} - 4}$ …

(1)、化简以上各式，并计算出结果；

(2)、以上格式的结果存在一定的规律，请按规律写出第5个式子及结果

(3)、用含n（n≥1的整数）的式子写出第n个式子及结果，并给出证明的过程．

查看试题解析
26. 解答下列问题：

(1)、
试比较与的大小；

(2)、
你能比较与的大小吗？其中k为正整数.

查看试题解析
27. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2 $\sqrt{2}$ ＝（1+ $\sqrt{2}$ ）² ．善于思考的小明进行了以下探索：
设a+b $\sqrt{2}$ ＝（m+n $\sqrt{2}$ ）²（其中a、b、m、n均为整数），则有a+b $\sqrt{2}$ ＝m²+2n²+2mn $\sqrt{2}$ ．

∴a＝m²+2n² ， b＝2mn．这样小明就找到了一种把类似a+b的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

(1)、当a、b、m、n均为正整数时，若a+b $\sqrt{5}$ ＝（m+n $\sqrt{5}$ ）² ，用含m、n的式子分别表示a、b，得：a＝， b＝；

(2)、利用探索的结论，找一组正整数a、b、m、n （a、b都不超过20）
填空：+ $\sqrt{7}$ ＝（+ $\sqrt{7}$ ）²；

(3)、若a+6 $\sqrt{3}$ ＝（m+n $\sqrt{3}$ ）² ，且a、m、n均为正整数，求a的值？

查看试题解析

2020年暑期衔接训练青岛版数学八年级下册：第15讲 第九章《二次根式》单元测试

一、单选题

二、填空题

三、解答题

2020年暑期衔接训练青岛版数学八年级下册：第15讲第九章《二次根式》单元测试