山西省晋中市2020年中考数学5月模拟试卷
试卷更新日期:2020-07-20 类型:中考模拟
一、单选题
-
1. |﹣5|的倒数等于( )A、 B、﹣5 C、﹣ D、52. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
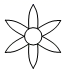 B、
B、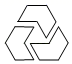 C、
C、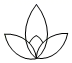 D、
D、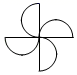 3. 如图所示,直线 、 、 、 的位置如图所示,若 , , ,则 的度数为
3. 如图所示,直线 、 、 、 的位置如图所示,若 , , ,则 的度数为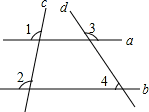 A、 B、 C、 D、4. 关于x的一元二次方程 ax2﹣3x﹣a=0 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断5.
A、 B、 C、 D、4. 关于x的一元二次方程 ax2﹣3x﹣a=0 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断5.如图所示正三棱柱的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 某种秋冬流感病毒的直径约为0.000000203米,该直径用科学记数法表示为( )米.A、2.03×10﹣8 B、2.03×10﹣7 C、2.03×10﹣6 D、0.203×10﹣67. 数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为( )
6. 某种秋冬流感病毒的直径约为0.000000203米,该直径用科学记数法表示为( )米.A、2.03×10﹣8 B、2.03×10﹣7 C、2.03×10﹣6 D、0.203×10﹣67. 数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为( )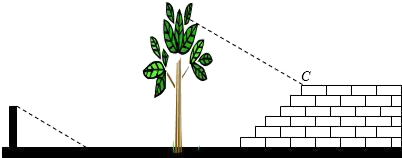 A、3.0m B、4.0m C、5.0m D、6.0m8. 如图,已知第一象限的点A在反比例函数y= 上,过点A作AB⊥AO交x轴于点B , ∠AOB=30°,将△AOB绕点O逆时针旋转120°,点B的对应点B恰好落在反比例函数y= 上,则k的值为( )
A、3.0m B、4.0m C、5.0m D、6.0m8. 如图,已知第一象限的点A在反比例函数y= 上,过点A作AB⊥AO交x轴于点B , ∠AOB=30°,将△AOB绕点O逆时针旋转120°,点B的对应点B恰好落在反比例函数y= 上,则k的值为( )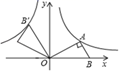 A、﹣4 B、﹣ C、﹣2 D、﹣9. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径面弧,两弧交于点 ,作射线 交边 于点 ,若 ,则 的面积是( )
A、﹣4 B、﹣ C、﹣2 D、﹣9. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径面弧,两弧交于点 ,作射线 交边 于点 ,若 ,则 的面积是( )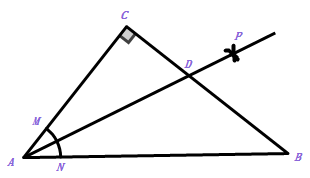 A、 B、 C、 D、10. 如图,点 、 、 在圆 上,若 , ,则图中阴影部分的面积是( )
A、 B、 C、 D、10. 如图,点 、 、 在圆 上,若 , ,则图中阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
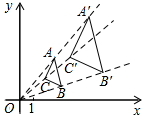
11. 方程x2=2020x的解是 .12. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为.
 13. 如图,四边形 为 的内接四边形,若四边形 为平行四边形,则 .
13. 如图,四边形 为 的内接四边形,若四边形 为平行四边形,则 .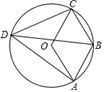 14. 如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为米.(结果保留两个有效数字)(参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601)
14. 如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为米.(结果保留两个有效数字)(参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601) 15. 如图,在矩形ABCD中,AB=9, ,点P是边BC上的动点(点P不与点B , 点C重合),过点P作直线PQ∥BD , 交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点,则∠CQP= .
15. 如图,在矩形ABCD中,AB=9, ,点P是边BC上的动点(点P不与点B , 点C重合),过点P作直线PQ∥BD , 交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点,则∠CQP= .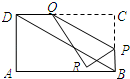
三、解答题
-
16.(1)、解方程(2)、计算17. 如图,在四边形ABCD中,对角线AC、BD交于点O , AB∥DC , AB=BC , BD平分∠ABC , 过点C作CE⊥AB交AB的延长线于点E , 连接OE .
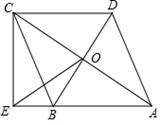 (1)、求证:四边形ABCD是菱形;(2)、若AB=2 ,BD=4,求OE的长.18. 如图,一次函数y1=x+4的图象与反比例函数y2= 的图象交于A(﹣1,a),B两点,与x轴交于点C .
(1)、求证:四边形ABCD是菱形;(2)、若AB=2 ,BD=4,求OE的长.18. 如图,一次函数y1=x+4的图象与反比例函数y2= 的图象交于A(﹣1,a),B两点,与x轴交于点C .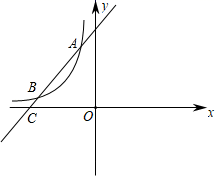 (1)、求k .(2)、根据图象直接写出y1>y2时,x的取值范围.(3)、若反比例函数y2= 与一次函数y1=x+4的图象总有交点,求k的取值.19. 现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.(1)、若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是;(2)、若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)20. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%。(1)、请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元。(2)、定价为多少时每天的利润最大?最大利润是多少?21. 操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC , AD=AE , 将这两个三角形放置在一起,使点B , D , E在同一直线上,连接CE .
(1)、求k .(2)、根据图象直接写出y1>y2时,x的取值范围.(3)、若反比例函数y2= 与一次函数y1=x+4的图象总有交点,求k的取值.19. 现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.(1)、若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是;(2)、若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)20. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%。(1)、请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元。(2)、定价为多少时每天的利润最大?最大利润是多少?21. 操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC , AD=AE , 将这两个三角形放置在一起,使点B , D , E在同一直线上,连接CE . (1)、如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;(2)、在(1)的条件下,求∠BEC的度数;(3)、拓广探索:如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.22. 如图,圆心在坐标原点的⊙O , 与坐标轴的交点分别为A、B和C、D . 弦CM交OA于P , 连结AM , 已知tan∠PCO= ,PC、PM是方程x2﹣px+20=0的两根.
(1)、如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;(2)、在(1)的条件下,求∠BEC的度数;(3)、拓广探索:如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.22. 如图,圆心在坐标原点的⊙O , 与坐标轴的交点分别为A、B和C、D . 弦CM交OA于P , 连结AM , 已知tan∠PCO= ,PC、PM是方程x2﹣px+20=0的两根.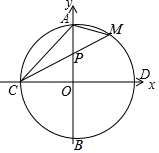 (1)、求C点的坐标;(2)、写出直线CM的函数解析式;(3)、求△AMC的面积.23. 如图,已知二次函数y=x2﹣2x+m的图象与x轴交于点A、B , 与y轴交于点C , 直线AC交二次函数图象的对称轴于点D , 若点C为AD的中点.
(1)、求C点的坐标;(2)、写出直线CM的函数解析式;(3)、求△AMC的面积.23. 如图,已知二次函数y=x2﹣2x+m的图象与x轴交于点A、B , 与y轴交于点C , 直线AC交二次函数图象的对称轴于点D , 若点C为AD的中点.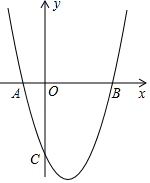 (1)、求m的值;(2)、若二次函数图象上有一点Q , 使得tan∠ABQ=3,求点Q的坐标;(3)、对于(2)中的Q点,在二次函数图象上是否存在点P , 使得△QBP∽△COA?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求m的值;(2)、若二次函数图象上有一点Q , 使得tan∠ABQ=3,求点Q的坐标;(3)、对于(2)中的Q点,在二次函数图象上是否存在点P , 使得△QBP∽△COA?若存在,求出点P的坐标;若不存在,请说明理由.