内蒙古呼和浩特市2020年中考数学4月模拟试卷

试卷更新日期：2020-07-20 类型：中考模拟

进入出卷网下载

一、单选题

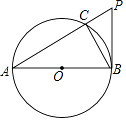
1. 下列四个实数中最大的是（）

A、 $\sqrt{5}$ B、0 C、1 D、-2

查看试题解析
2. 下列说法正确的是（　　）

A、某事件发生的概率为0，则该事件不可能发生 B、一种彩票中奖率为千分之一，那么买一千张彩票就一定能中奖 C、调查一批灯泡的使用寿命可以采取普遍调查的方式进行 D、掷一枚骰子两次，掷得的点数之和可能等于8

查看试题解析
3. 我国珠港澳大桥闻名世界，它东起香港国际机场附近的香港口岸人工岛，向西横跨南海伶仃洋水域接珠海和澳门人工岛，止于珠海洪湾立交，工程项目总投资1269亿元．用科学记数法表示1269亿正确的是（）

A、 $1.269 \times 10^{3}$ B、 $1.269 \times 10^{8}$ C、 $1.269 \times 10^{11}$ D、 $1.269 \times 10^{12}$

查看试题解析
4. 下列计算正确的是（　　）

A、a³+a²=a⁵ B、3a^﹣2= $\frac{1}{3 a^{2}}$ C、a⁶b÷a²=a³b D、（﹣ab³）²=a²b⁶

查看试题解析
5. 如图，这是一块直角三角形的空地，计划将阴影部分修建围花圃，已知AC长为8米，AB长为17米，阴影部分是三角形的内切圆．一只小鸟随机落在这块绿化带上，则小鸟落在花圃上的概率是（　　）

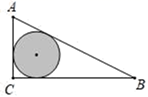A、 $\frac{3}{20} π$ B、 $\frac{3}{10} π$ C、 $\frac{3}{20}$ D、 $\frac{3}{10}$

查看试题解析
6. 如图是由几个相同的小正方体搭成的几何体的主视图和俯视图，则搭成这个几何体的小正方体的个数最少是（　　）

A、6 B、8 C、10 D、12

查看试题解析
7. 小明家1至6月份的用水量统计如图所示，则5月份的用水量比4月份增加的百分率为（）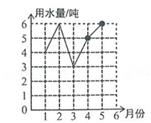

A、25％ B、20％ C、50％ D、33％

查看试题解析
8. 已知点（－2，y₁），（－1，y₂），（1，y₃）都在反比例函数y= $- \frac{6}{x}$ 的图象上，那么y₁ ， y₂与y₃的大小关系是

A、y₃＜y₁＜y₂ B、y₃＜y₂＜y₁ C、y₁＜y₂＜y₃ D、y₁＜y₃＜y₂

查看试题解析
9. 下列命题是真命题的是（　　）

A、多边形的内角和为360° B、若2a﹣b＝1，则代数式6a﹣3b﹣3＝0 C、二次函数y＝（x﹣1）²+2的图象与y轴的交点的坐标为（0，2） D、矩形的对角线互相垂直平分

查看试题解析
10. 已知a是两位数，b是一位数，把a接写在b的后面，就成为一个三位数．这个三位数可表示成（　　）

A、10b+a B、ba C、100b+a D、b+10a

查看试题解析

二、填空题

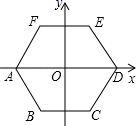
11. 代数式 $\frac{1}{\sqrt{x + 8}}$ 有意义时，x应满足的条件是．

查看试题解析
12. 如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若点A的坐标为（﹣2，0），则AB＝，点C的坐标为．

查看试题解析
13. 二次函数y＝x²﹣6x+k的图象与x轴有交点，则k的取值范围是．

查看试题解析
14. 因式分解：ax³y﹣axy³＝．

查看试题解析
15. 将关于x的一元二次方程x²+px+q＝0变形为x²＝﹣px﹣q ，就可将x²表示为关于x的一次多项式，从而达到“降次”的目的，我们称这样的方法为“降次法”，已知x²﹣x﹣1＝0，可用“降次法”求得x⁴﹣3x+2014的值是．

查看试题解析
16. x ， y为实数，且满足 $y = \frac{2 x + 2}{x^{2} + 3 x + 3}$ ，则y的最大值是．

查看试题解析

三、解答题

17.

(1)、先化简，再求值：（2﹣ $\frac{x - 1}{x + 1}$ ）÷ $\frac{x^{2} + 6 x + 9}{x^{2} - 1}$ ，其中x＝2．

(2)、计算：| $\sqrt{3}$ ﹣2|+2010⁰﹣（﹣ $\frac{1}{3}$ ）^﹣¹+3tan30°．

查看试题解析
18. 如图，在平行四边形ABCD中，E、F是对角线BD上的两点，且BF=DE.
求证：AE∥CF.

查看试题解析
19. 已知关于x的不等式组 ${\begin{array}{l} x < m + 2 \\ 3 x - 5 ⩾ m \end{array}$ 的解集中恰好有两个整数，求m的取值范围．

查看试题解析
20. 为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
身高情况分组表（单位：cm）
组别
身高
A
x＜155
B
155≤x＜160
C
160≤x＜165
D
165≤x＜170
E
x≥170
根据图表提供的信息，回答下列问题：

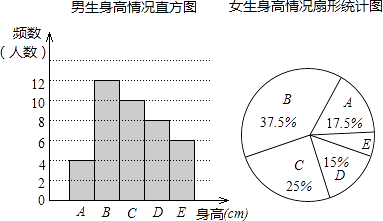(1)、样本中，男生的身高众数在组，中位数在组；

(2)、样本中，女生身高在E组的人数有人；

(3)、已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？

查看试题解析
21. 国家推行“节能减排，低碳经济”政策后，低排量的汽车比较畅销，某汽车经销商购进A、B两种型号的低排量汽车，其中A型汽车的进货单价比B型汽车的进货单价多2万元；花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同．

(1)、求A，B两种型号汽车的进货单价；

(2)、销售中发现A型汽车的每周销量y_A（台）与售价x（万元/台）满足函数关系y_A＝﹣x+20，B型汽车的每周销量y_B（台）与售价x（万元/台）满足函数关系y_B＝﹣x+14，A型汽车的售价比B型汽车的售价高2万元/台．问A、B两种型号的汽车售价各为多少时，每周销售这两种汽车的总利润最大？最大利润是多少万元？

查看试题解析
22. 已知，如图，在坡顶A处的同一水平面上有一座古塔BC，数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°，然后他们沿着坡度为1：2.4的斜坡AP攀行了26米，在坡顶A处又测得该塔的塔顶B的仰角为76°.求：

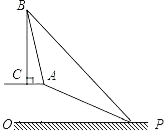(1)、坡顶A到地面PO的距离；

(2)、古塔BC的高度（结果精确到1米）.
（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）

查看试题解析
23. 如图，一次函数y₁＝﹣x﹣1的图象与x轴交于点A，与y轴交于点B，与反比例函数 $y_{2} = \frac{k}{x}$ 图象的一个交点为M（﹣2，m）.

(1)、求反比例函数的解析式；

(2)、当y₂＞y₁时，求x的取值范围；

(3)、求点B到直线OM的距离.

查看试题解析
24. 如图，AB是⊙O的直径，PB与⊙O相切于点B，连接PA交⊙O于点C，连接BC．

(1)、求证：∠BAC=∠CBP；

(2)、求证：PB²=PC•PA；

(3)、当AC=6，CP=3时，求sin∠PAB的值．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 2 a x - 3 a_{_{}} {_{}}^{} (a \neq 0)$ ，与x轴交于A、B两点(点A在点B的左侧).

(1)、求点A和点B的坐标；

(2)、若点P（m，n）是抛物线上的一点，过点P作x轴的垂线，垂足为点D.
①在 $a > 0$ 的条件下，当 $- 2 \leq m \leq 2$ 时，n的取值范围是 $- 4 \leq n \leq 5$ ，求抛物线的表达式；

②若D点坐标（4，0），当 $P D > A D$ 时，求a的取值范围.

查看试题解析

组别	身高
A	x＜155
B	155≤x＜160
C	160≤x＜165
D	165≤x＜170
E	x≥170