江西省上饶市玉山县2020年中考数学一模试卷

试卷更新日期：2020-07-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 2的相反数是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $2$ D、 $- 2$

查看试题解析
2. 如图所示物体的俯视图是（）

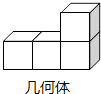A、 B、 C、 D、

查看试题解析
3. 计算 ${(- \frac{1}{2} x y^{2})}^{3}$ 结果正确的是（）

A、 $\frac{1}{6} x^{2} y^{4}$ B、 $- \frac{1}{8} x^{3} y^{6}$ C、 $\frac{1}{6} x^{3} y^{6}$ D、 $- \frac{1}{8} x^{3} y^{5}$

查看试题解析
4. 方程x²﹣3x＝0的根是（）

A、x＝0 B、x＝3 C、 $x_{1} = 0$ ， $x_{2} = - 3$ D、 $x_{1} = 0$ ， $x_{2} = 3$

查看试题解析
5.
在2014年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数、方差依次是（）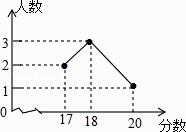

A、18，18，1 B、18，17.5，3 C、18，18，3 D、18，17.5，1

查看试题解析
6. “如果二次函数y=ax²+bx+c的图象与x轴有两个公共点，那么一元二次方程ax²+bx+c=0有两个不相等的实数根．”请根据你对这句话的理解，解决下面问题：若m、n（m＜n）是关于x的方程1﹣（x﹣a）（x﹣b）=0的两根，且a＜b，则a、b、m、n的大小关系是（）．

A、 $m < a < b < n$ B、 $a < m < n < b$ C、 $a < m < b < n$ D、 $m < a < n < b$

查看试题解析

二、填空题

7. 命题“同旁内角互补”是一个命题（填“真”或“假”）

查看试题解析
8. 我国最长的河流——长江全长约为6300千米，用科学记数法可表示为千米．

查看试题解析
9. 若关于x的一元二次方程 $x^{2} + 2 x - k = 0$ 没有实数根，则k的取值范围是．

查看试题解析
10. 分解因式：mn²﹣6mn+9m= ．

查看试题解析
11. 线段AB、CD在平面直角坐标系中位置如图所示，O为坐标原点．若线段AB上一点P的坐标为(a、b)，则直线OP与线段CD的交点坐标为．

查看试题解析
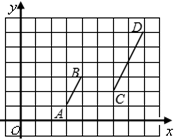12. 在直角坐标系中，如图有△ABC，现另有一点D满足以A、B、D为顶点的三角形与△ABC全等，则D点坐标为．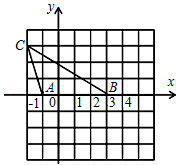

查看试题解析

三、解答题

13.

(1)、 $| - 1 | - \frac{1}{2} \sqrt{8} - {(5 - π)}^{0} + 4 \cos 45 °$ ；

(2)、解方程： $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$ ．

查看试题解析
14. 如图，AE为菱形ABCD的高，请仅用无刻度的直尺按要求画图.（不写画法，保留画图痕迹）.

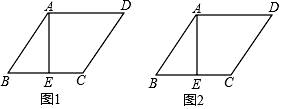(1)、在图1中，过点C画出AB边上的高；

(2)、在图2中，过点C画出AD边上的高.

查看试题解析
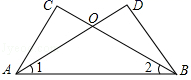
15. 先化简（1﹣ $\frac{x}{x - 1}$ ）÷ $\frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，再从不等式x﹣1≤2的正整数解中选一个适当的数代入求值．

查看试题解析
16. 如图，△ABC与△ABD中，AD与BC相交于O点，∠1=∠2，请你添加一个条件（不再添加其它线段，不再标注或使用其他字母），使AC=BD，并给出证明．
你添加的条件是：．

查看试题解析
17. 某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：(100m，200m，400m分别用A₁、A₂、A₃表示)；田赛项目：跳远，跳高（分别用B₁、B₂表示）

(1)、该同学从5个项目中任选一个，恰好是田赛项目的概率为；

(2)、该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率．

查看试题解析
18. 一艘轮船由南向北航行，如图，在A处测得小岛P在北偏西15°方向上，两个小时后，轮船在B处测得小岛P在北偏西30°方向上，在小岛周围18海里内有暗礁，问若轮船按20海里/时的速度继续向北航行，有无触礁的危险？

查看试题解析
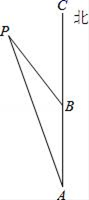19. 如图，一次函数y＝kx+b的图象与反比例函数y＝ $\frac{m}{x}$ 的图象交于A（﹣2，1），B（1，n）两点．

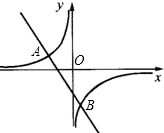(1)、求反比例函数和一次函数的解析式；

(2)、根据图象写出使一次函数的值＞反比例函数的值的x的取值范围．

查看试题解析
20. 国家规定“中小学生每天在校体育活动时间不低于1小时”．为此，某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生．根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：

A组： ${\begin{matrix} ( a ， -b ) \\ ( -a ， b ) \\ ( -a ， -b ) \end{matrix}$ ； B组： $0.5 h \leq t < 1 h$

C组： $1 h \leq t < 1.5 h$ D组： $t \geq 1.5 h$

请根据上述信息解答下列问题：

(1)、C组的人数是；

(2)、本次调查数据的中位数落在组内；

(3)、若该辖区约有24 000名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？

查看试题解析
21. 在平面直角坐标系中，△AOB的位置如图所示，已知∠AOB=90°，AO=BO，点A的坐标为(-3，1)．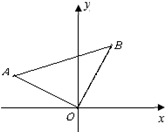

(1)、求点B的坐标；

(2)、求过A、O、B三点的抛物线的解析式；

(3)、设点B关于抛物线的对称轴 $l$ 的对称点为B₁ ，求△AB₁B的面积．

查看试题解析
22. 已知：如图①，②，在矩形ABCD中，AB=4，BC=8，P，Q分别是边BC，CD上的点．

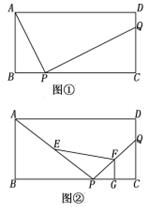(1)、如图①，若AP⊥PQ，BP=2，求CQ的长；

(2)、如图②，若 $\frac{B P}{C Q}$ =2，且E，F，G分别为AP，PQ，PC的中点，求四边形EPGF的面积．

查看试题解析
23. 如图①，②，在平面直角坐标系xOy中，点A的坐标为(4，0)，以点A为圆心，4为半径的圆与x轴交于O，B两点，OC为弦，∠AOC=60°，P是x轴上的一动点，连结CP．

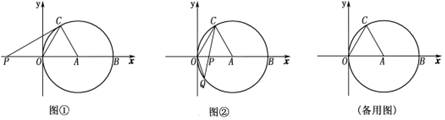(1)、求∠OAC的度数；

(2)、如图①，当CP与⊙A相切时，求PO的长；

(3)、如图②，当点P在直径OB上时，CP的延长线与⊙A相交于点Q，问PO为何值时，△OCQ是等腰三角形？

查看试题解析