江西省萍乡市安源区2020年中考数学二模试卷

试卷更新日期：2020-07-20 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{2}{3}$ 的倒数是（　　）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{3} \cdot a^{2} = a^{5}$ C、 ${(2 a^{2})}^{3} = 6 a^{6}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
3. 下列调查中，调查方式选择正确的是（　　）

A、为了了解某品牌手机的屏幕是否耐摔，选择全面调查 B、为了了解玉兔号月球车的零部件质量，选择抽样调查 C、为了了解端午节期间市场上的粽子质量，选择全面调查 D、为了了解步行街平均每天的人流量，选择抽样调查

查看试题解析
4. 如图，把△ $A B C$ 沿 $E F$ 对折，叠合后的图形如图所示.若 $∠ A = 60 °$ ， $∠ 1 = 95 °$ ，则∠2的度数为（）

A、24° B、35° C、30° D、25°

查看试题解析
5. 均匀地向一个容器注水，最后将容器注满，在注水的过程中，水的高度h随时间t的变化如图所示，这个容器的形状可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图是一个螺母的示意图，它的俯视图是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 分解因式： $x^{2} - 4 =$ .

查看试题解析
8. 今年世界各地发现新冠肺炎疫情，疫情是由一种新型冠状病毒引起的，疫情发生后，科学家第一时间采集了病毒样本进行研究.研究发现这种病毒的直径约85纳米（1纳米＝0.000000001米）.数据85纳米用科学记数法可以表示为米．

查看试题解析
9. 如图，l∥m，等腰直角三角形ABC的直角顶点C在直线m上，若∠β=35°，则∠α的度数为．

查看试题解析
10. 已知m+n=3mn，则 $\frac{1}{m}$ + $\frac{1}{n}$ 的值为．

查看试题解析
11. 如图，直线过正方形ABCD的顶点B，点A、C到直E的距离分别是1和2，则正方形ABCD面积是.

查看试题解析
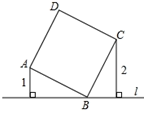12. 抛物线表达式C： $y = \frac{1}{12} (x + 1) (x - 4)$ ，已知点A(0，2)，点P是抛物线上一点，若Rt△AOP有一个锐角正切值为 $\frac{1}{2}$ ，则点P的坐标．

查看试题解析

三、解答题

13.

(1)、计算： ${(\sqrt{3})}^{0} - {(\frac{1}{2})}^{- 2} + \tan 45 °$

(2)、如图，已知∠CAE是△ABC的外角，∠1＝∠2，AD∥BC，求证：AB＝AC.

查看试题解析
14. 解方程： $1 - \frac{3}{2 - x} = \frac{5 - x}{x - 2}$

查看试题解析

15. 事业单位人员编制连进必考，现一事业单位需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表：

	笔试	面试	体能
甲	84	80	88
乙	94	92	69
丙	81	84	78

(1)、根据三项得分的平均分，从高到低确定三名应聘者的排名顺序；

(2)、该单位规定：笔试、面试、体能分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分.根据规定，请你说明谁将被录用.

查看试题解析

16. 如图，△ABC内接于⊙O，AB＝AC，D是AC弧的中点，在下列图中使用无刻度的直尺按要求画图．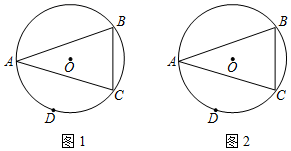

(1)、在图1中，画出△ABC中AC边上的中线；

(2)、在图2中，画出△ABC中AB边上的中线．

查看试题解析
17. 今年我国许多地方严重的“旱情”，为了鼓励居民节约用水，区政府计划实行两级收费制，即每月用水量不超过14吨（含14吨）时，每吨按政府补贴优惠价收费；每月超过14吨时，超过部分每吨按市场调节价收费．小英家1月份用水20吨，交水费29元；2月份用水18吨，交水费24元．

(1)、求每吨水的政府补贴优惠价和市场调节价分别是多少？

(2)、设每月用水量为x吨，应交水费为y元，写出y与x之间的函数关系式．

查看试题解析

18. 某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制例图1、图2两幅均不完整的统计图表．

校本课程	频数	频率
A	36	0.45
B		0.25
C	16	b
D	8
合计	a	1

请您根据图表中提供的信息回答下列问题：

(1)、统计表中的a＝， b＝；

(2)、“D”对应扇形的圆心角为度；

(3)、根据调查结果，请您估计该校2000名学生中最喜欢“数学史”校本课程的人数；

(4)、小明和小亮参加校本课程学习，若每人从“A”、“B”、“C”三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．

查看试题解析

19. 如图，△ABC中，D是AB边上一点，⊙O过D、B、C三点，∠DOC=2∠ACD=90°．

(1)、求证：直线AC是⊙O的切线；

(2)、如果∠ACB=75°，⊙O的半径为2，求BD的长．

查看试题解析
20. 如图1是一台放置在水平桌面上的笔记本电脑，将其侧面抽象成如图2所示的几何图形.若显示屏AO与键盘BO长均为24cm，点P为眼睛所在位置，D为AO的中点，连接PD，且PD⊥AO（此时点P为最佳视角），点C在OB的延长线上，PC⊥BC，BC＝12cm.

(1)、当PA＝45cm时，求PC的长；

(2)、当∠AOC＝115°时，线段PC的长比（1）中线段PC的长是增大还是减小？请通过计算说明．（结果精确到0.1cm，sin65°≈0.91，cos65°≈0.42，tan65°≈2.14，sin25°≈0.42，cos25°≈0.91，tan25°≈0.47）.

查看试题解析
21. 如图，一次函数y＝kx＋b的图象与反比例函数y＝ $\frac{m}{x}$ (x＞0)的图象交于点P(n，2)，与x轴交于点A(－4，0)，与y轴交于点C，PB⊥x轴于点B，点A与点B关于y轴对称．

(1)、求一次函数，反比例函数的表达式；

(2)、求证：点C为线段AP的中点；

(3)、反比例函数图象上是否存在点D，使四边形BCPD为菱形．如果存在，说明理由并求出点D的坐标；如果不存在，说明理由．

查看试题解析
22. 如图，矩形ABCD中，∠ACB=30°，将一块直角三角板的直角顶点P放在两对角线AC，BD的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别与边AB，BC所在的直线相交，交点分别为E，F．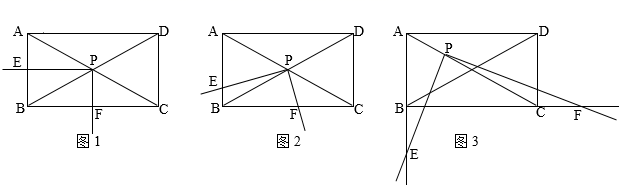

(1)、当PE⊥AB，PF⊥BC时，如图1，则 $\frac{P E}{P F}$ 的值为　　；

(2)、在（1）的基础上，现将三角板绕点P逆时针旋转α（0°＜α＜60°）角，如图2，求 $\frac{P E}{P F}$ 的值；

(3)、若与（2）相比只有如下变化，点P在线段AC上，且AP：PC=1：2，旋转角度α，满足60°＜α＜90°时，即如图3示， $\frac{P E}{P F}$ 的值是否变化？证明你的结论．

查看试题解析
23. 已知抛物线 $C_{1} ： y_{1} = a （ x － 1 ）^{2} + k_{1} （ a \neq 0 ）$ 交x轴于点（0，0）和点 $A_{1} （ b_{1} ， 0 ）$ ，抛物线 $C_{2} ： y_{2} = a （ x － b_{1} ）^{2} + k_{2}$ 交x轴于点（0，0）和点 $A_{2} （ b_{2} ， 0 ）$ ，抛物线 $C_{3} ： y_{3} = a （ x － b_{2} ）^{2} + k_{3}$ 交x轴于点（0，0）和点 $A_{3} （ b_{3} ， 0 ）$ …按此规律，抛物线 $C_{n} ： y_{n} = a （ x － b_{n}_{﹣ 1} ）^{2} + k_{n}$ 交x轴于点（0，0）和点 $A_{n} （ b_{n} ， 0 ）$ （其中n为正整数），我们把抛物线 $C_{1} ， C_{2} ， C_{3} \dots ， C_{n}$ 称为系数为a的“关于原点位似”的抛物线族．

(1)、试求出b₁的值；

(2)、请用含n的代数式表示线段 $A_{n}_{﹣ 1} A_{n}$ 的长；

(3)、探究下列问题：
①抛物线 $C_{n} ： y_{n} = a （ x － b_{n}_{﹣ 1} ）^{2} + k_{n}$ 的顶点纵坐标 $k_{n}$ 与a、n有何数量关系？请说明理由；

②若系数为a的“关于原点位似”的抛物线族的各顶点坐标记为（T，S），请直接写出S和T所满足的函数关系式．

查看试题解析