江西省南昌市2020年中考数学二模试卷

试卷更新日期：2020-07-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，绝对值最大的是（）

A、2 B、-2 C、 $\sqrt{3}$ D、-3

查看试题解析
2. 计算a^﹣³•（﹣a²）的结果是（　　）

A、﹣a⁵ B、﹣a² C、 $- \frac{1}{a}$ D、a^﹣⁵

查看试题解析
3. 已知一种户外帐篷的几何体及其主视图如图所示，则它的左视图为（）

A、 B、 C、 D、

查看试题解析
4. 统计数据显示，2019年，我省数字产业营收近6000亿元，数字经济逐渐成为我省创新创业的主战场．数据6000亿用科学记数法可表示为（）

A、 $0.6 \times 10^{12}$ B、 $6 \times 10^{11}$ C、 $6 \times 10^{10}$ D、 $60 \times 10^{10}$

查看试题解析
5. 已知矩形的长和宽是方程 $x^{2} - 7 x + 8 = 0$ 的两个实数根，则矩形的对角线的长为（）

A、 $6$ B、 $7$ C、 $\sqrt{41}$ D、 $\sqrt{33}$

查看试题解析
6. 如图，正方形 $A B C D$ 的边长为3cm一个边长为1cm的小正方形沿着正方形 $A B C D$ 的边 $A B \to B C \to C D \to D A$ 连续翻转(小正方形起始位置在 $A B$ 边上)，当这个小正方形翻转到 $D A$ 边的终点位置时，它的方向是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 因式分解：4x²﹣y²＝.

查看试题解析
8. 已知一组数据 $4 ， 3 ， 2 ， m ， n$ 的众数为3，平均数为 $2 ， m > n$ ，则n的值为．

查看试题解析
9. 如图，AB∥CD ， Rt△EFG的直角顶点E在直线AB上，且EF交CD于点P ，若∠BEG＝52°，则∠CPF的度数为．

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $∠ B A D = 45 ° ， D E$ 是 $A B$ 边上的高， $B E = 1 ，$ 则菱形的面积为．

查看试题解析
11. 我国古代数学著作(九章算术)中有如下问题：“今有人持金出五关，前关二而税一．次关三而税一，次关四而税一，次关五而税一，次关六而税一，并五关所税，适重一斤．”其意思为“今有人持金出五关，第1关所收税金为持金的 $\frac{1}{2}$ ，第2关所收税金为剩余金的 $\frac{1}{3}$ ，第3关所收税金为剩余金的 $\frac{1}{4}$ ，第4关所收税金为剩余金的 $\frac{1}{5}$ ，第5关所收税金为剩余金的 $\frac{1}{6}$ ，5关所收税金之和，恰好重1斤．”若设这个人原本持金x斤，根据题意可列方程为．

查看试题解析
12. 已知矩形AOBC的边AO、OB分别在y轴、x轴正半轴上，点C的坐标为（8，6），点E是x轴上任意一点，连接EC ，交AB所在直线于点F ，当△ACF为等腰三角形时，EF的长为．

查看试题解析

三、解答题

13.

(1)、计算： $- 1^{2020} - 2 \times {(- 3)}^{2} + \sqrt[3]{- 27} \div (- \frac{1}{3})$ ．

(2)、解不等式： $x - 2 \geq \frac{x + 1}{2} + 3$ ．

查看试题解析
14. 如图，在平行四边形 $A F C E$ 中， $D ， B$ 分别是 $E C ， A F$ 的中点．求证： $B C = A D$ ．

查看试题解析
15. 读高中的小明从家到学校需要中途转一趟车，从家到站台M可乘 $A ， B ， C$ 三路车(小明乘 $A ， B ， C$ 三路车的可能性相同)，到了站台M后可以转乘D路或E路车直接到学校(小明乘 $D ， E$ 两路车的可能性相同)．

(1)、“小明从家到站台M乘坐A路车”是事件，小明从站台M到学校乘坐F路车的概率为_

(2)、请用列表或画树状图的方法，求小明先乘坐A路车，再转乘D路或E路车到学校的概率．

查看试题解析
16. 如图，在网格纸中，O、A都是格点，以O为圆心， $O A$ 为半径作圆，用无刻度的直尺完成以下画图：（不写画法）

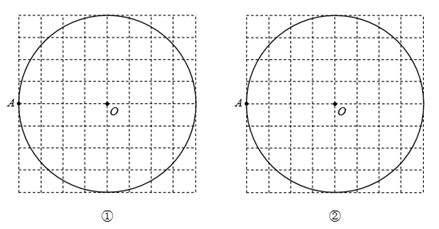(1)、在圆①中画圆O的一个内接正六边形 $A B C D E F$ ；

(2)、在图②中画圆O的一个内接正八边形 $A B C D E F G H$ .

查看试题解析
17. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象与反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象交于 $A (1 ， t + 1) ， B (t - 5 ， - 1)$ 两点．

(1)、求一次函数和反比例函数的解析式；

(2)、若 $(c ， p) ， (n ， q)$ 是反比例函数 $y = \frac{m}{x} (m \neq 0)$ 图象上任意两点，且满足 $c = n + 1$ ，求 $\frac{q - p}{p q}$ 的值．

查看试题解析

18. 某校为了调查学生对卫生健康知识，特别是疫情防控下的卫生常识的了解，现从九年级1000名学生中随机抽取了部分学生参加测试，并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整)．

组别	成绩 $x$ /分	人数
第1组	$x < 60$	$20$
第2组	$60 \leq x < 70$	$a$
第3组	$70 \leq x < 80$	$100$
第4组	$80 \leq x < 90$	$65$
第5组	$90 \leq x < 100$	$b$

请结合图表信息完成下列各题．

(1)、表中a的值为， b的值为；在扇形统计图中，第1组所在扇形的圆心角度数为°；

(2)、若测试成绩不低于80分为优秀，请你估计从该校九年级学生中随机抽查一个学生，成绩为优秀的概率．

(3)、若测试成绩在60分以上(含60分)均为合格，其他为不合格，请你估计该校九年级学生中成绩不合格的有多少人．

查看试题解析

19. 如图，已知AB为半圆O的直径，过点B作PB⊥OB，连接AP交半圆O于点C，D为BP上一点，CD是半圆O的切线．

(1)、求证：CD＝DP．

(2)、已知半圆O的直径为 $\sqrt{6}$ ，PC＝1，求CD的长．

查看试题解析
20. 如今，不少人在购买家具时追求简约大气的风格，图1所示的是一款非常畅销的简约落地收纳镜，其支架的形状固定不变，镜面可随意调节，图2所示的是其侧面示意图，其中 $O D$ 为镜面， $E F$ 为放置物品的收纳架， $A B ， A C$ 为等长的支架， $B C$ 为水平地面，已知 $O A = 44 c m ， O D = 120 c m ， B D = 40 c m$ ， $∠ A B C = 75 °$ ．(结果精确到 $1 c m$ ．参考数据： $s i n 75 ° \approx 0.97 ， c o s 75 ° \approx 0.26 ， t a n 75 ° \approx 3.73 ， \sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ )

(1)、求支架顶点A到地面 $B C$ 的距离．

(2)、如图3，将镜面顺时针旋转15°求此时收纳镜顶部端点O到地面 $B C$ 的距离．

查看试题解析

21. 如图1，在

R t △ A B C

中，D为

A B

的中点，P是

B C

边上一动点，连接

P D ， P A

．若

B C = 4 ， A C = 3 ，

设

P C = x

(当点P与点C重合时，x的值为0)，

P A + P D = y

．

小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

下面是小明的探究过程，请补充完整．

(1)、通过取点、画图、计算，得到了x与y的几组值，如下表：

$x$	$0$	$0.5$	$1$	$1.5$	$2$	$2.5$	$3$	$3.5$	$4$
$y$	$5.5$	$5.15$		$4.94$	$5.1$	$5.5$		$6.7$	$7.5$

说明：补全表格时，相关数值保留一位小数．

(参考数据： $\sqrt{2} \approx 1.414 ， \sqrt{10} \approx 3.162 ， \sqrt{13} \approx 3.606$ ) ．

(2)、如图2，描出剩余的点，并用光滑的曲线画出该函数的图象．

(3)、观察图象，下列结论正确的有_ ．

①函数有最小值，没有最大值

②函数有最小值，也有最大值

③当 $x > \frac{4}{3}$ 时，y随着x的增大而增大

④当 $x < 1.5$ 时，y随着x的增大而减小

查看试题解析

22. 如图，抛物线 $y = x^{2} - (a + 1) x + a$ 与x轴交于 $A ， B$ 两点(点A位于点B的左侧)，与y轴的负半轴交于点C．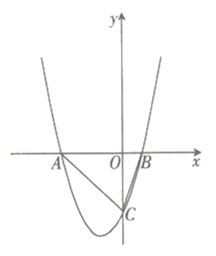

(1)、求点B的坐标．

(2)、若 $△ A B C$ 的面积为6．
①求这条抛物线相应的函数解析式．

②在拋物线上是否存在一点P使得 $∠ P O B = ∠ C B O$ ？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析
23. 定义：有一组对角互补的四边形叫做互补四边形．

(1)、概念理解：
在互补四边形 $A B C D$ 中， $∠ A$ 与 $∠ C$ 是一组对角，若 $∠ B ： ∠ C ： ∠ D = 2 ： 3 ： 4 ，$ 则 $∠ A =$ $^{\circ}$

(2)、如图1，在 $△ A B C$ 中，点 $D ， E$ 分别在边 $A B ， B C$ 上，且 $B E \cdot B C = A B \cdot B D ，$ 求证：四边形 $A D E C$ 是互补四边形．

(3)、探究发现：如图2，在等腰 $△ A B E$ 中， $A E = B E ，$ 点 $C ， D$ 分别在边 $B E ， A E$ 上， $A D = B C ，$ 四边形 $C E D H$ 是互补四边形，求证： $∠ A B D = ∠ B A C = \frac{1}{2} ∠ E$ ．

(4)、推广运用：如图3，在 $△ A B E$ 中，点 $C ， D$ 分别在边 $B E ， A E$ 上， $A D = B C ，$ 四边形 $C E D H$ 是互补四边形，若 $∠ E = 60 ° ， A B = 6 ， A E = \frac{20}{3}$ ，求 $\frac{D H}{C E}$ 的值．

查看试题解析