江西省吉安吉州区2020年中考数学模拟试卷
试卷更新日期:2020-07-20 类型:中考模拟
一、单选题
-
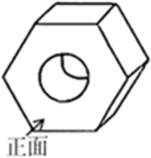
1. 的相反数是( )A、 B、2 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 空心六棱柱螺母按如图所示位置摆放,则它的左视图正确的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式组 的解集在数轴上表示正确的是( )A、
4. 不等式组 的解集在数轴上表示正确的是( )A、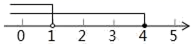 B、
B、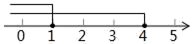 C、
C、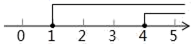 D、
D、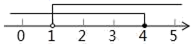 5. 在如图所示的网格中,已知线段AB,现要在该网格内再确定格点C和格点D,某数学探究小组在探究时发现以下结论:以下结论错误的是( )
5. 在如图所示的网格中,已知线段AB,现要在该网格内再确定格点C和格点D,某数学探究小组在探究时发现以下结论:以下结论错误的是( )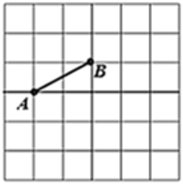 A、将线段 平移得到线段 ,使四边形 为正方形的有2种; B、将线段 平移得到线段 ,使四边形 为菱形的(正方形除外)有3种; C、将线段 平移得到线段 ,使四边形 为矩形的(正方形除外)有两种; D、不存在以 为对角线的四边形 是菱形.6. 如图,直线 交x轴、y轴于A、B两点,点P为线段AB上的点,过点P作 轴于点E,作 轴于点F, ,将线段AB沿y轴负方向向下移动a个单位,线段 扫过矩形 的面积为Z,则下图描述Z与a的函数图象可能是( )
A、将线段 平移得到线段 ,使四边形 为正方形的有2种; B、将线段 平移得到线段 ,使四边形 为菱形的(正方形除外)有3种; C、将线段 平移得到线段 ,使四边形 为矩形的(正方形除外)有两种; D、不存在以 为对角线的四边形 是菱形.6. 如图,直线 交x轴、y轴于A、B两点,点P为线段AB上的点,过点P作 轴于点E,作 轴于点F, ,将线段AB沿y轴负方向向下移动a个单位,线段 扫过矩形 的面积为Z,则下图描述Z与a的函数图象可能是( )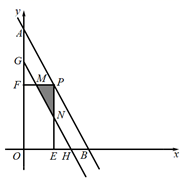 A、
A、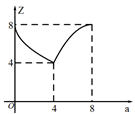 B、
B、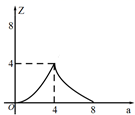 C、
C、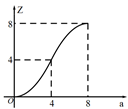 D、
D、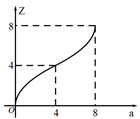
二、填空题
-
7. 据统计,为支持打赢打好脱贫攻坚战,江西省财政厅下达2019年中央财政专项扶贫资金总额为30.8亿元,30.8亿用科学记数法可表示为.8. 如图, , 平分 ,直尺与 垂直,则∠1等于.
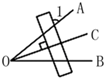 9. 一元二次方程 的两根为 , ,则 的值为.10. 《九章算术》第九章勾股篇中记载:“今有开门去阃( )一尺,不合二寸,问门广几何?”其大意是:今推开双门,门框到门槛的距离(称为“去阃”) 为一尺,双门之间的缝隙(称为“不合”) 为2寸(注:一尺为10寸),则门宽 为尺.
9. 一元二次方程 的两根为 , ,则 的值为.10. 《九章算术》第九章勾股篇中记载:“今有开门去阃( )一尺,不合二寸,问门广几何?”其大意是:今推开双门,门框到门槛的距离(称为“去阃”) 为一尺,双门之间的缝隙(称为“不合”) 为2寸(注:一尺为10寸),则门宽 为尺.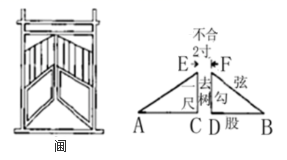 11. 有2020个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是a,第二个数是b,那么这2020个数的和是.12. 已知等腰 内接于半径为5的 ,已知圆心O到 的距离为3,则这个等腰 中底边上的高可能是.
11. 有2020个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是a,第二个数是b,那么这2020个数的和是.12. 已知等腰 内接于半径为5的 ,已知圆心O到 的距离为3,则这个等腰 中底边上的高可能是.三、解答题
-
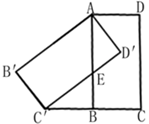
13.(1)、计算:(2)、如图,将矩形 绕点A顺时针旋转,得到矩形 ,点C的对应点 恰好落在 的延长线上,边 交边 于点E,求证:
 14. 已知 .(1)、先化简A,再从1、2、3、-3中选一个合适的数作为 的值代入求值.(2)、若 ,求x的值;15. 如图已知二次函数 的图象及对称轴,限用无刻度直尺按下列要求作图:
14. 已知 .(1)、先化简A,再从1、2、3、-3中选一个合适的数作为 的值代入求值.(2)、若 ,求x的值;15. 如图已知二次函数 的图象及对称轴,限用无刻度直尺按下列要求作图: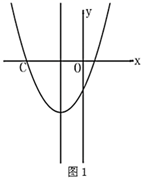
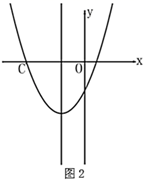 (1)、在图1中作点 ;(2)、已知 ,在图2中的对称轴上作点P,使 最大;16. 为做好新型肺炎疫情防控,某社区开展新型肺炎疫情排查与宣传教育志愿服务活动,组织社区20名志愿者随机平均分配在4个院落门甲、乙、丙、丁处值守,并对进出人员进行测温度、劝导佩戴口罩、符合题意投放生活垃圾等服务.(1)、志愿者小明被分配到甲处服务是( )事件;A、不可能事件 B、可能事件 C、必然事件 D、无法确定(2)、请用列表或树状图的方法,求出志愿者小明和小红被随机分配到同一处服务的概率.17. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。(1)、求购买一个足球、一个篮球各需多少元?(2)、根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?18. 为做好新型肺炎疫情防控,某街道组织社区200名志愿者开展新型肺炎疫情排查与宣传教育志愿服务活动,为了了解18~68岁各年龄段志愿者对本次新型肺炎疫情排查与宣传教育志愿服务的参与程度,随机选取了100名年龄在该范围内的志愿者进行了调查,并将收集到的数据制成了尚不完整的频数分布表,如下所示:
(1)、在图1中作点 ;(2)、已知 ,在图2中的对称轴上作点P,使 最大;16. 为做好新型肺炎疫情防控,某社区开展新型肺炎疫情排查与宣传教育志愿服务活动,组织社区20名志愿者随机平均分配在4个院落门甲、乙、丙、丁处值守,并对进出人员进行测温度、劝导佩戴口罩、符合题意投放生活垃圾等服务.(1)、志愿者小明被分配到甲处服务是( )事件;A、不可能事件 B、可能事件 C、必然事件 D、无法确定(2)、请用列表或树状图的方法,求出志愿者小明和小红被随机分配到同一处服务的概率.17. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。(1)、求购买一个足球、一个篮球各需多少元?(2)、根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?18. 为做好新型肺炎疫情防控,某街道组织社区200名志愿者开展新型肺炎疫情排查与宣传教育志愿服务活动,为了了解18~68岁各年龄段志愿者对本次新型肺炎疫情排查与宣传教育志愿服务的参与程度,随机选取了100名年龄在该范围内的志愿者进行了调查,并将收集到的数据制成了尚不完整的频数分布表,如下所示:组别
年龄段
频数(人数)
频率
第1组
5
5%
第2组
25%
第3组
35
第4组
20
第5组
15
15%
 (1)、请直接写出a= , m=.(2)、现该市有18~68岁的志愿者约有10000人,求第3组年龄段的志愿者人数约有多少?(3)、如果这200名志愿者在该社区所占的比例如扇形统计图所示,求该社区估计有多少人?(4)、社区的部分果农、菜农自发踊跃捐助了一车的水果和蔬菜共8吨慰问社区志愿者助力社区疫情防控,其中定向捐助每个志愿者的水果与蔬菜之比是3:1,求该社区每个志愿者将分别得到多少千克的水果与蔬菜?19. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示,由两根有槽的棒 , 组成,两根棒在O点相连并可绕O转动.C点固定, ,点D,E可在槽中滑动,
(1)、请直接写出a= , m=.(2)、现该市有18~68岁的志愿者约有10000人,求第3组年龄段的志愿者人数约有多少?(3)、如果这200名志愿者在该社区所占的比例如扇形统计图所示,求该社区估计有多少人?(4)、社区的部分果农、菜农自发踊跃捐助了一车的水果和蔬菜共8吨慰问社区志愿者助力社区疫情防控,其中定向捐助每个志愿者的水果与蔬菜之比是3:1,求该社区每个志愿者将分别得到多少千克的水果与蔬菜?19. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示,由两根有槽的棒 , 组成,两根棒在O点相连并可绕O转动.C点固定, ,点D,E可在槽中滑动,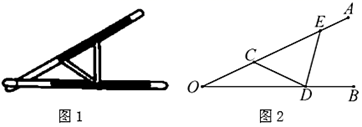 (1)、求证: .(2)、若 ,
(1)、求证: .(2)、若 ,①求 的度数;
②求点D到 的距离.
(参考数据: , , , , , )
20. 已知点O是菱形 对角线 上的点,以点O为圆心, 为半径的圆与 相切于点C.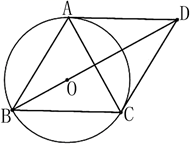 (1)、求证: 与 相切;(2)、若圆O的半径为6,求菱形的边长;21. 如图1,线段 及一定点C,P是线段 上一动点(A、B除外),作直线 ,使 于点C,作直线 ,使 于点D.已知 , ,设 , ,数学学习小组根据学习函数的经验,对y与x之间的内在关系进行探究.
(1)、求证: 与 相切;(2)、若圆O的半径为6,求菱形的边长;21. 如图1,线段 及一定点C,P是线段 上一动点(A、B除外),作直线 ,使 于点C,作直线 ,使 于点D.已知 , ,设 , ,数学学习小组根据学习函数的经验,对y与x之间的内在关系进行探究.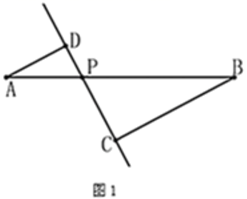 (1)、写出y与x之间的关系和x的取值范围;(2)、①列表,根据(1)的所求函数关系式讲算并补全表格
(1)、写出y与x之间的关系和x的取值范围;(2)、①列表,根据(1)的所求函数关系式讲算并补全表格0.5
1
1.5
2
2.5
3
3.5
1.8
9
21
②描点:根据表格中数值,继续在图2中描出剩余的三个点 ;
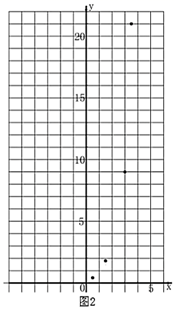
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考:
(3)、请你结合函数的图象,写出该函数的一条性质或结论.(4)、将该函数图象向上移3个单位,再向左平移4个单位后,直接写出平移后的函数关系式和x的取值范围.22. 已知菱形 中, 为对角线,点F是 的中点,连接 交 于点E, 的垂直平分线 交 于点G,交 于点H,连接 .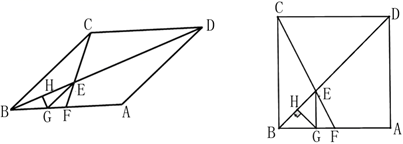 (1)、若 ,求证:四边形 是正方形(2)、已知 ,求 的长;(3)、若 固定,设 ,将 绕着点B从点A开始逆时针旋转过程中,菱形 也随之变化,且 满足 ,若 是直角三角形,直接写出 的值;23. 已知抛物线L: ,其中 .(1)、以下结论正确的序号有;
(1)、若 ,求证:四边形 是正方形(2)、已知 ,求 的长;(3)、若 固定,设 ,将 绕着点B从点A开始逆时针旋转过程中,菱形 也随之变化,且 满足 ,若 是直角三角形,直接写出 的值;23. 已知抛物线L: ,其中 .(1)、以下结论正确的序号有;①抛物线的对称轴是直线 ; ②抛物线经过定点 , ;
③函数y随着x的增大而减小; ④抛物线的顶点坐标为 .
(2)、将抛物线L向右平移k个单位得到抛物线 .①若抛物线L与抛物线 关于y轴对称,求抛物线 的解析式;
②抛物线 顶点的纵坐标 与横坐标x之间存在一个函数关系,求这个函数关系式,并写出x的取值范围;
③若抛物线L与 轴交于点B,抛物线 的顶点为A,求 之间的最小距离.