江西省赣州市寻乌县2020年中考数学一模试卷
试卷更新日期:2020-07-20 类型:中考模拟
一、单选题
-
1. 下列关于0的说法正确的是( )A、0是正数 B、0是负数 C、0是有理数 D、0是无理数2. 下列几何体中,其侧面展开图为扇形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、“367人中必有2人的生日是同一天”是必然事件 B、了解一批灯泡的使用寿命采用全面调查 C、一组数据6,5,3,5,4的众数是5,中位数是3 D、一组数据10,11,12,9,8的平均数是10,方差是1.54. 实数 、 在数轴上的对应点的位置如图所示,下列式子成立的是( )
3. 下列说法正确的是( )A、“367人中必有2人的生日是同一天”是必然事件 B、了解一批灯泡的使用寿命采用全面调查 C、一组数据6,5,3,5,4的众数是5,中位数是3 D、一组数据10,11,12,9,8的平均数是10,方差是1.54. 实数 、 在数轴上的对应点的位置如图所示,下列式子成立的是( ) A、 B、 C、 D、5. 如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )
A、 B、 C、 D、5. 如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= 上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…Sn.则Sn可表示为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= 上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…Sn.则Sn可表示为( )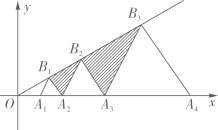 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 分别写有数字 、﹣1、0、π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是 .8. 当b+c=5时,关于x的一元二次方程3x2+bx﹣c=0的根的情况为 .9. 若一组数据x , 3,1,6,3的中位数和平均数相等,则x的值为 .10. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾 ,弦 ,则小正方形ABCD的面积是.
 11. 已知圆锥的底面半径是1,高是 ,则该圆锥的侧面展开图的圆心角是度.12. 如图,在矩形ABCD中, , ,点E在边BC上,且 .连接AE,将 沿AE折叠,若点B的对应点 落在矩形ABCD的边上,则a的值为.
11. 已知圆锥的底面半径是1,高是 ,则该圆锥的侧面展开图的圆心角是度.12. 如图,在矩形ABCD中, , ,点E在边BC上,且 .连接AE,将 沿AE折叠,若点B的对应点 落在矩形ABCD的边上,则a的值为. 13. 如图,正方形ABCD中, ,点P在BC上运动(不与B、C重合),过点P作 ,交CD于点Q,则CQ的最大值为 .
13. 如图,正方形ABCD中, ,点P在BC上运动(不与B、C重合),过点P作 ,交CD于点Q,则CQ的最大值为 .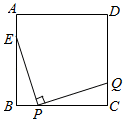
三、解答题
-
14. 计算: tan30°-(π-2019)0;15. 先化简,再求值: ,其中 , .16. 如图,一次函数 (k1、b为常数,k1≠0)的图象与反比例函数 的图象交于点A(m,8)与点B(4,2).
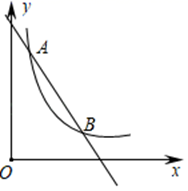
①
(1)、求一次函数与反比例函数的解析式.(2)、根据图象说明,当x为何值时, .17. 在 6×6 的方格纸中,点 A,B,C 都在格点上,按要求画图: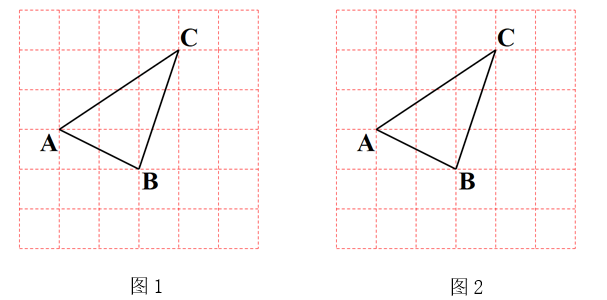 (1)、在图1中找一个格点D,使以点 A,B,C,D 为顶点的四边形是平行四边形.(2)、在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).18. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?19. “扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)、在图1中找一个格点D,使以点 A,B,C,D 为顶点的四边形是平行四边形.(2)、在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).18. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?19. “扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: (1)、接受问卷调查的学生共有人,扇形统计图中“很了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.20. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.
(1)、接受问卷调查的学生共有人,扇形统计图中“很了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.20. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.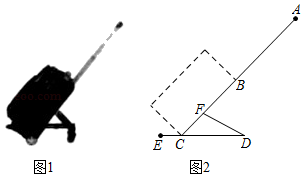 (1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).21. 如图,在矩形ABCD中,CD=2,AD=4,点P在BC上,将△ABP沿AP折叠,点B恰好落在对角线AC上的E点.O为AC上一点,⊙O经过点A , P .
(1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).21. 如图,在矩形ABCD中,CD=2,AD=4,点P在BC上,将△ABP沿AP折叠,点B恰好落在对角线AC上的E点.O为AC上一点,⊙O经过点A , P . (1)、求证:BC是⊙O的切线;(2)、在边CB上截取CF=CE , 点F是线段BC的黄金分割点吗?请说明理由.22. (阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
(1)、求证:BC是⊙O的切线;(2)、在边CB上截取CF=CE , 点F是线段BC的黄金分割点吗?请说明理由.22. (阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.(理解):
(1)、如图,两个边长分别为a、b、c的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论; (2)、如图2,n行n列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(2)、如图2,n行n列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ; (3)、(运用): n边形有n个顶点,在它的内部再画m个点,以( )个点为顶点,把n边形剪成若干个三角形,设最多可以剪得y个这样的三角形.当 , 时,如图,最多可以剪得7个这样的三角形,所以 .
(3)、(运用): n边形有n个顶点,在它的内部再画m个点,以( )个点为顶点,把n边形剪成若干个三角形,设最多可以剪得y个这样的三角形.当 , 时,如图,最多可以剪得7个这样的三角形,所以 .
①当 , 时,如图, ;当 , 时, ;

②对于一般的情形,在n边形内画m个点,通过归纳猜想,可得 (用含m、n的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
23. 如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C , 过点C作CD⊥y轴交抛物线于另一点D , 作DE⊥x轴,垂足为点E , 双曲线y= (x>0)经过点D , 连接MD , BD .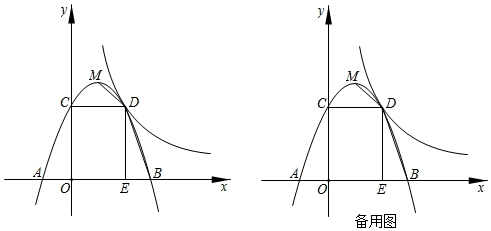 (1)、求抛物线的表达式;(2)、点N , F分别是x轴,y轴上的两点,当以M , D , N , F为顶点的四边形周长最小时,求出点N , F的坐标;(3)、动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
(1)、求抛物线的表达式;(2)、点N , F分别是x轴,y轴上的两点,当以M , D , N , F为顶点的四边形周长最小时,求出点N , F的坐标;(3)、动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?