福建省三明市2020年中考数学二模试卷

试卷更新日期：2020-07-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数在数轴上表示的点到原点的距离最近的是（）

A、-1 B、－ $\frac{1}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
2. 如图所示的几何体是由5个大小相同的小立方块搭成，其左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 新型冠状病毒的直径约为0.000 000 12米，把0.000 000 12用科学记数法表示为（　　）

A、0.12×10^-6 B、1.2×10^-6 C、1.2×10^-7 D、12×10^-8

查看试题解析
4. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $3 a^{2} + a = 3 a^{3}$ C、 $a^{5} \div a^{2} = a^{3} (a \neq 0)$ D、 $a (a + 1) = a^{2} + 1$

查看试题解析
5. 小红同学对数据25，32，23，25，4■，43进行统计分析，发现“4■”的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（　　）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
6. 如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，若AD=8，∠B=30°，则AC的长度为（　　）

A、3 B、4 C、4 $\sqrt{2}$ D、 $4 \sqrt{3}$

查看试题解析
7. 在平面直角坐标系中，若一个正比例函数的图象经过A（m，6），B（5，n）两点，则m，n一定满足的关系式为（　　）

A、m－n=1 B、m＋n=11 C、 $\frac{m}{n}$ = $\frac{6}{5}$ D、 $m n = 30$

查看试题解析
8. 已知抛物线y=ax²+bx-2(a＞0)过A(-2，y₁)，B(-3，y₂)，C(1，y₂)，D( $\sqrt{3}$ ，y₃)四点，则y₁ ， y₂ ， y₃的大小关系是(　　)

A、y₁＞y₂＞y₃ B、y₂＞y₁＞y₃ C、y₁＞y₃＞y₂ D、y₃＞y₂＞y₁

查看试题解析
9. 如图，在菱形ABCD中，CE⊥AD于点E，cosD= $\frac{3}{5}$ ，AE=4，则AC的长为（　）

A、8 B、 $4 \sqrt{5}$ C、 $4 \sqrt{10}$ D、 $4 \sqrt{13}$

查看试题解析
10. 如图，在平面直角坐标系中，O为▱ABCD的对称中心，点A的坐标为(－2，－2)，AB=5，AB//轴，反比例函数y= $\frac{k}{x}$ 的图象经过点D，将▱ABCD沿y轴向下平移，使点C的对应点C′落在反比例函数的图象上，则平移过程中线段AC扫过的面积为(　　)

A、10 B、18 C、20 D、24

查看试题解析

二、填空题

11. $2^{3} - \sqrt{4}$ ＝．

查看试题解析
12. 如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=52°，则∠2= °．

查看试题解析
13. 小明要用如图的两个转盘做“配紫色”游戏（红色和蓝色配成紫色），每个转盘均被等分成若干个扇形，他同时转动两个转盘，停止时指针所指的颜色恰好配成紫色的概率为．

查看试题解析
14. 我国古代数学著作《九章算术》有一道关于买田的问题：“今有善田一亩，价三百；恶田一亩，价五十．今并买顷，价钱一万，问善田恶田各几何？”其意思是“好田300钱一亩，坏田50钱一亩，合买好田、坏田100亩，共需10000钱，问好田、坏田各买了多少亩？”设好田买了x亩，坏田买了y亩，可列方程组为．

查看试题解析
15. 如图，在扇形AOB中，∠AOB=90°，半径OA=4．将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点C处，折痕交OA于点D，则图中阴影部分的面积为．

查看试题解析
16. 如图，△PAB中，PA=3，PB=4，以AB为边作等边△ABC，则点P、C间的距离的最大值为．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 3 (x - 1) \geq 2 x - 4 \\ \frac{x}{3} < \frac{x + 1}{4} \end{array}$ 并把它的解集表示在数轴上．

查看试题解析
18. 如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD∥BC.求证：四边形ABCD是平行四边形.

查看试题解析
19. 先化简 $(x + 3 - \frac{7}{x - 3}) \div \frac{2 x^{2} - 8 x}{x - 3}$ ，再从 $0 \leq x \leq 4$ 中选一个适合的整数代入求值.

查看试题解析
20. 如图，直升飞机在大桥AB上方C点处测得A，B两点的俯角分别为45°和31°．若飞机此时飞行高度CD为1205m，且点A，B，D在同一条直线上，求大桥AB的长．(精确到1m)(参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60)

查看试题解析
21. 如图，已知△ABC中，AB＝AC．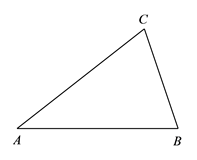

(1)、把△ABC绕点C顺时针旋转得到△DEC，使得点B的对应点E落在AB边上，用尺规作图的方法作出△DEC；（保留作图痕迹，不写作法）

(2)、在（1）的条件下，连接AD，求证：AD＝BC．

查看试题解析
22. 某服装店计划购进一批甲、乙两种款式的运动服进行销售，进价和售价如下表所示：

运动服款式

甲

乙

进价（元/套）

80

100

售价（元/套）

120

160

若购进两种款式的运动服共300套，且投入资金不超过26800元．

(1)、该服装店应购进甲款运动服至少多少套？

(2)、若服装店购进甲款运动服的进价每套降低a元，并保持这两款运动服的售价不变，且最多购进240套甲款运动服．如果这批运动服售出后，服装店刚好获利18480元，求a的取值范围．

查看试题解析

23. 随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯．由此催生了一批外卖点餐平台，已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调査送餐员的送餐收入，现从该平台随机抽取80名点外卖的用户进行统计，按送餐距离分类统计结果如下表：

送餐距离x（千米）	0 $<$ x $\leq$ 1	1 $<$ x $\leq$ 2	2 $<$ x $\leq$ 3	3 $<$ x $\leq$ 4	4 $<$ x $\leq$ 5
数量	12	20	24	16	8

(1)、从这80名点外卖的用户中任取一名用户，该用户的送餐距离不超过3千米的概率为；

(2)、以这80名用户送餐距离为样本，同一组数据取该小组数据的中间值（例如第二小组（1＜x ≤2）的中间值是1.5），试估计利用该平台点外卖用户的平均送餐距离；

(3)、若该外卖平台给送餐员的送餐费用与送餐距离有关，不超过2千米时，每份3元；超过2千米但不超4千米时，每份5元；超过4千米时，每份9元．以给这80名用户所需送餐费用的平均数为依据，若送餐员一天的目标收入不低于150元，试估计一天至少要送多少份外卖？

查看试题解析

24. 如图，在△ABC中，∠ACB=90°，AC=3，BC=1，点D是斜边上一点，且AD=4BD．

(1)、求tan∠BCD的值；

(2)、过点B的⊙O与边AC相切，切点为AC的中点E，⊙O与直线BC的另一个交点为F．
(ⅰ)求⊙O的半径；

(ⅱ) 连接AF，试探究AF与CD的位置关系，并说明理由．

查看试题解析
25. 如图，抛物线y=x²+mx（m<0）交x轴于O，A两点，顶点为点B．

(1)、求△AOB的面积（用含m的代数式表示）；

(2)、直线y=kx+b（k＞0）过点B，且与抛物线交于另一点D（点D与点A不重合），交y轴于点C．过点C作CE∥AB交x轴于点E．
（ⅰ）若∠OBA=90°，2< $\frac{C E}{A B}$ <3，求k的取值范围；

（ⅱ）求证：DE∥y轴．

查看试题解析

运动服款式	甲	乙
进价（元/套）	80	100
售价（元/套）	120	160