福建省福州市2020年中考数学二模试卷
试卷更新日期:2020-07-20 类型:中考模拟
一、单选题
-
1. 在实数 , ,2.02002, 中,无理数的是( )A、 B、 C、2.02002 D、2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算中,结果可以为 的是( )A、 B、 C、 D、4. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形5. 若 ,其中a为整数,则a的值是( )A、1 B、2 C、3 D、46. 《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为 ,买鸡的钱数为 ,可列方程组为( )A、 B、 C、 D、7. 随机调查某市100名普通职工的个人年收入(单位:元)情况,得到这100人年收入的数据,记这100个数据的平均数为a,中位数为b,方差为c.若将其中一名职工的个人年收入数据换成世界首富的年收入数据,则a一定增大,那么对b与c的判断正确的是( )A、b一定增大,c可能增大 B、b可能不变,c一定增大 C、b一定不变,c一定增大 D、b可能增大,c可能不变8. 若一个粮仓的三视图如图所示(单位:m),则它的体积(参考公式:圆锥: ,圆柱: )是( )
3. 下列运算中,结果可以为 的是( )A、 B、 C、 D、4. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形5. 若 ,其中a为整数,则a的值是( )A、1 B、2 C、3 D、46. 《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为 ,买鸡的钱数为 ,可列方程组为( )A、 B、 C、 D、7. 随机调查某市100名普通职工的个人年收入(单位:元)情况,得到这100人年收入的数据,记这100个数据的平均数为a,中位数为b,方差为c.若将其中一名职工的个人年收入数据换成世界首富的年收入数据,则a一定增大,那么对b与c的判断正确的是( )A、b一定增大,c可能增大 B、b可能不变,c一定增大 C、b一定不变,c一定增大 D、b可能增大,c可能不变8. 若一个粮仓的三视图如图所示(单位:m),则它的体积(参考公式:圆锥: ,圆柱: )是( )
 A、 B、 C、 D、9. 如图,在菱形 中,点E是 的中点,以C为圆心, 长为半径作 ,交 于点F,连接 , .若 , ,则阴影部分的面积是( )
A、 B、 C、 D、9. 如图,在菱形 中,点E是 的中点,以C为圆心, 长为半径作 ,交 于点F,连接 , .若 , ,则阴影部分的面积是( ) A、 B、 C、 D、10. 小明在研究抛物线 ( 为常数)时,得到如下结论,其中正确的是( )A、无论x取何实数,y的值都小于0 B、该抛物线的顶点始终在直线 上 C、当 时,y随x的增大而增大,则 D、该抛物线上有两点 , ,若 , ,则
A、 B、 C、 D、10. 小明在研究抛物线 ( 为常数)时,得到如下结论,其中正确的是( )A、无论x取何实数,y的值都小于0 B、该抛物线的顶点始终在直线 上 C、当 时,y随x的增大而增大,则 D、该抛物线上有两点 , ,若 , ,则二、填空题
-
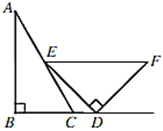
11. 计算: .12. 能够成为直角三角形三条边长的三个正整数称为勾股数.若从2,3,4,5中任取3个数,则这3个数能构成一组勾股数的概率是 .13. 一副三角尺如图摆放,D是 延长线上一点,E是 上一点, , , ,若 ∥ ,则 等于度.
 14. 若 ,则 的值是 .15. 如图,在 中,C是弧 的中点,作点C关于弦 的对称点D,连接 并延长交 于点E,过点B作 于点F,若 ,则 等于度.
14. 若 ,则 的值是 .15. 如图,在 中,C是弧 的中点,作点C关于弦 的对称点D,连接 并延长交 于点E,过点B作 于点F,若 ,则 等于度.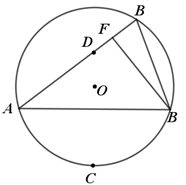 16. 如图,在平面直角坐标系 中, 的顶点A,B分别在x,y轴的负半轴上,C,D在反比例函数 ( )的图象上, 与y轴交于点E,且 ,若 的面积是3,则k的值是 .
16. 如图,在平面直角坐标系 中, 的顶点A,B分别在x,y轴的负半轴上,C,D在反比例函数 ( )的图象上, 与y轴交于点E,且 ,若 的面积是3,则k的值是 .
三、解答题
-
17. 解不等式组 ,并把它的解集在数轴上表示出来.
 18. 如图,点E,F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
18. 如图,点E,F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.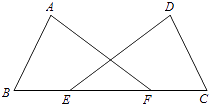 19. 先化简,再求值: ,其中 .20. 如图,已知 ,A,B分别是射线 , 上的点.
19. 先化简,再求值: ,其中 .20. 如图,已知 ,A,B分别是射线 , 上的点.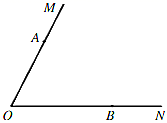 (1)、尺规作图:在 的内部确定一点C,使得 且 ;(保留作图痕迹,不写作法)(2)、在(1)中,连接 ,用无刻度直尺在线段 上确定一点D,使得 ,并证明 .21. 甲,乙两人从一条长为200m的笔直栈道两端同时出发,各自匀速走完该栈道全程后就地休息.图1是甲出发后行走的路程y(单位:m)与行走时间x(单位: )的函数图象,图2是甲,乙两人之间的距离s(单位:m)与甲行走时间x(单位: )的函数图象.
(1)、尺规作图:在 的内部确定一点C,使得 且 ;(保留作图痕迹,不写作法)(2)、在(1)中,连接 ,用无刻度直尺在线段 上确定一点D,使得 ,并证明 .21. 甲,乙两人从一条长为200m的笔直栈道两端同时出发,各自匀速走完该栈道全程后就地休息.图1是甲出发后行走的路程y(单位:m)与行走时间x(单位: )的函数图象,图2是甲,乙两人之间的距离s(单位:m)与甲行走时间x(单位: )的函数图象. (1)、求甲,乙两人的速度;(2)、求a,b的值.22. 某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案:一户家庭的月均用水量不超过m(单位:t)的部分按平价收费,超出m的部分按议价收费.为此拟召开听证会,以确定一个合理的月均用水量标准m.通过抽样,获得了前一年1000户家庭每户的月均用水量(单位:t),将这1000个数据按照 , ,…, 分成8组,制成了如图所示的频数分布直方图.
(1)、求甲,乙两人的速度;(2)、求a,b的值.22. 某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案:一户家庭的月均用水量不超过m(单位:t)的部分按平价收费,超出m的部分按议价收费.为此拟召开听证会,以确定一个合理的月均用水量标准m.通过抽样,获得了前一年1000户家庭每户的月均用水量(单位:t),将这1000个数据按照 , ,…, 分成8组,制成了如图所示的频数分布直方图. (1)、写出a的值,并估计这1000户家庭月均用水量的平均数;(同一组中的数据以这组数据所在范围的组中值作代表)(2)、假定该市政府希望70%的家庭的月均用水量不超过标准m,请判断若以(1)中所求得的平均数作为标准m是否合理?并说明理由.23. 如图,在 中, , ,以 为直径作 交 于点D,E是 的中点,连接 .点F在 上,连接 并延长交 的延长线于点G.
(1)、写出a的值,并估计这1000户家庭月均用水量的平均数;(同一组中的数据以这组数据所在范围的组中值作代表)(2)、假定该市政府希望70%的家庭的月均用水量不超过标准m,请判断若以(1)中所求得的平均数作为标准m是否合理?并说明理由.23. 如图,在 中, , ,以 为直径作 交 于点D,E是 的中点,连接 .点F在 上,连接 并延长交 的延长线于点G. (1)、求证: 是 的切线;(2)、连接 ,求 的最大值.24. 已知 , , ,D是 边上一点,连接 ,E是 上一点,且 .(1)、如图1,若 ,
(1)、求证: 是 的切线;(2)、连接 ,求 的最大值.24. 已知 , , ,D是 边上一点,连接 ,E是 上一点,且 .(1)、如图1,若 ,
①求证: 平分∠ ;
②求 的值;
(2)、如图2,连接 ,若 ,求 的值. 25. 在平面直角坐标系 中,抛物线C: 的对称轴是y轴,过点 作一直线与抛物线C相交于P,Q两点,过点Q作x轴的垂线与直线 相交于点A.(1)、求抛物线C的解析式;(2)、判断点A是否在直线 上,并说明理由;(3)、若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线C上的任意一点(除顶点外)作该抛物线的切线l,分别交直线 和直线 于点M,N,求 的值.
25. 在平面直角坐标系 中,抛物线C: 的对称轴是y轴,过点 作一直线与抛物线C相交于P,Q两点,过点Q作x轴的垂线与直线 相交于点A.(1)、求抛物线C的解析式;(2)、判断点A是否在直线 上,并说明理由;(3)、若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线C上的任意一点(除顶点外)作该抛物线的切线l,分别交直线 和直线 于点M,N,求 的值.