内蒙古开鲁县2020年中考数学一模试卷

试卷更新日期：2020-07-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个数中，-2020的倒数是（）

A、2020 B、 $2020^{- 1}$ C、 $- \frac{1}{2020}$ D、 $- 2020$

查看试题解析
2. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为（）

A、 $46 \times 10^{- 7}$ B、 $4.6 \times 10^{- 7}$ C、 $4.6 \times 10^{- 6}$ D、 $0.46 \times 10^{- 5}$

查看试题解析
3. 下列图形中是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 设边长为3的正方形的对角线长为a，下列关于a的四种说法：① a是无理数；② a可以用数轴上的一个点来表示；③ 3<a<4；④ a是18的算术平方根．其中，所有符合题意说法的序号是

A、①④ B、②③ C、①②④ D、①③④

查看试题解析
5. 如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积为（）

A、10π B、14π C、18π D、20π

查看试题解析
6. 已知▱ABCD，根据图中尺规作图的痕迹，判断下列结论中不一定成立的是（）

A、∠DAE＝∠BAE B、∠DEA＝ $\frac{1}{2}$ ∠DAB C、DE＝BE D、BC＝DE

查看试题解析
7. 如图，小正方形的边长均为1，有格点△ABC，则sinC=（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
8. 如图，⊙O的半径为4，AB，CD是互相垂直的两条直径，点P是⊙O上任意一点，过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P从点A运动到点D时，点Q所经过的路径长为（）

A、 $\frac{π}{2}$ B、 $π$ C、 $\frac{3 π}{2}$ D、 $2 π$

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图，则一次函数 $y = a x + b c$ 与反比例函数 $y = \frac{a b c}{x}$ 在平面直角坐标系中的图象可能是（）．

A、 B、 C、 D、

查看试题解析
10. 如图，正方形ABCD中，AB=6，E为AB的中点，将△ADE沿DE翻折得到△FDE，延长EF交BC于G， FH⊥BC，垂足为H，连接BF、DG．以下结论：①BF∥ED； ②△DFG ≌△DCG；③△FHB∽△EAD；④tan∠GEB= $\frac{4}{3}$ ；⑤S_△_BFG=2.4．其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

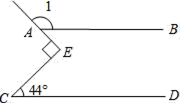
11. 函数y= $\frac{\sqrt{2-x}}{x + 1}$ 中，自变量x的取值范围是.

查看试题解析
12. 如图，直线AB∥CD，∠C＝44°，∠E为直角，则∠1＝.

查看试题解析
13. 若一组数据 $4, x, 5, y, 7, 9$ 的平均数为6，众数为5，则这组数据的方差为．

查看试题解析
14. 从满足不等式组 ${\begin{array}{l} 2 x + 1 \leq 7 \\ 3 x - 2 > - 11 \end{array}$ 的所有整数解中任意取一个数记作a ，则关于 $y$ 的一元二次方程 $a y^{2} - y - \frac{3}{4} = 0$ 有实数根的概率是．

查看试题解析
15. 已知矩形ABCD，对角线AC、BD相交于点O，点E为BD上一点，OE＝1，连接AE，∠AOB＝60°，AB＝2，则AE的长为．

查看试题解析
16. 如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为4，2，反比例函数y＝ $\frac{k}{x}$ (x＞0)的图象经过A，B两点，若菱形ABCD的面积为2 $\sqrt{5}$ ，则k的值为.

查看试题解析
17. 按一定规律排列的一列数依次为： $- \frac{a^{2}}{2}$ ， $\frac{a^{5}}{5}$ ， $- \frac{a^{8}}{10}$ ， $\frac{a^{11}}{17}$ ，…(a≠0)，按此规律排列下去，这列数中的第n个数是.(n为正整数)

查看试题解析

三、解答题

18. 计算： ${(π - 2020)}^{0} - | \sqrt{12} - 4 | + {(\frac{1}{3})}^{- 1} - 2 \tan 60 °$

查看试题解析
19. 先化简： $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$ ，并从 $0 \leq x \leq 4$ 中选取合适的整数代入求值．

查看试题解析
20. 为积极参与鄂州市全国文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图.小明同学为测量宣传牌的高度AB，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°（A、B、D、E在同一直线上）.然后，小明沿坡度i=1：1.5的斜坡从C走到F处，此时DF正好与地面CE平行.

(1)、求点F到直线CE的距离(结果保留根号)；

(2)、若小明在F处又测得宣传牌顶部A的仰角为45°，求宣传牌的高度AB（结果精确到0.1米， $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）.

查看试题解析

21. “停课不停学，学习不延期”，某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”，为了解学生每天的学习时间情况，在全市随机抽取了部分初中学生进行问卷调查，现将调查结果绘制成如下不完整的统计图表，请根据图表中的信息解答下列问题：

组别	学习时间x（h）	人数（人）
A	2.5＜x≤3	40
B	3＜x≤3.5	170
C	3.5＜x≤4	350
D	4＜x≤4.5
E	4.5＜x≤5	90
F	5小时以上	50

表1

(1)、这次参与问卷调查的初中学生有人，中位数落在组．

(2)、图3中D组对应的角度是，并补全图2 条形统计图．

(3)、若某市有初中学生2.8万人，请估计每天参与“空中课堂”学习时间3.5到4.5小时（不包括3.5小时）的初中学生有多少人？

查看试题解析

22. 为落实立德树人的根本任务，加强思政、历史学科教师的专业化队伍建设．某校计划从前来应聘的思政专业（两名研究生，一名本科生）、历史专业（一名研究生、两名本科生）的高校毕业生中选聘教师，在政治思想审核合格的条件下，假设每位毕业生被录用的机会相等．

(1)、若从中只录用一人，恰好选到思政专业毕业生的概率是；

(2)、若从中录用两人，请用列表或画树状图的方法，求恰好选到的是一名思政研究生和一名历史研究生的概率．

查看试题解析
23. 如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．

(1)、求证：△ABF≌△CBE；

(2)、判断△CEF的形状，并说明理由．

查看试题解析
24. 如图①，某新建火车站站前广场需要绿化的面积为35000 $m^{2}$ ，施工队在绿化了11000 $m^{2}$ 后，将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．

(1)、该项绿化工程原计划每天完成多少平方米？

(2)、该项绿化工程中有一块长为20m、宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56 $m^{2}$ ，两块绿地之间及周边留有宽度相等的人行通道（如图②所示），则人行通道的宽度是多少米？

查看试题解析
25. 如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC＝PC，∠COB＝2∠PCB．

(1)、求证：PC是⊙O的切线；

(2)、点M是 $\overset{⌢}{A B}$ 的中点，CM交AB于点N，若AB＝6，求MN•MC的值．

查看试题解析
26. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ 交 $x$ 轴于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，交 $y$ 轴于点 $C (0 ， 6)$ ，在 $y$ 轴上有一点 $E (0 ， - 2)$ ，连接 $A E$ .

(1)、求二次函数的表达式；

(2)、若点 $D$ 为抛物线在 $x$ 轴负半轴上方的一个动点，求 $Δ A D E$ 面积的最大值；

(3)、抛物线对称轴上是否存在点 $P$ ，使 $Δ A E P$ 为等腰三角形，若存在，请直接写出所有 $P$ 点的坐标，若不存在请说明理由.

查看试题解析