人教版数学八年级下册第十九章 一次函数测试卷
试卷更新日期:2020-07-19 类型:单元试卷
一、单选题
-
1. 下列各曲线中,不表示y是 x的函数的是( )A、
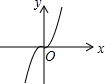 B、
B、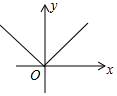 C、
C、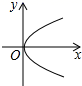 D、
D、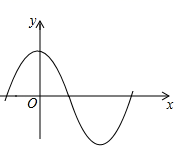 2. 下列函数:(1) y=x ;(2) ;(3) ;(4) ;(5)s=12t;(6)y=30-4x中,是一次函数的有 ( )A、2个 B、3个 C、4个 D、5个3. 函数
2. 下列函数:(1) y=x ;(2) ;(3) ;(4) ;(5)s=12t;(6)y=30-4x中,是一次函数的有 ( )A、2个 B、3个 C、4个 D、5个3. 函数 的图象一定经过点( ) A、(3,5) B、(-2,3) C、(2,7) D、(4,10)4. y=kx+(k-3)的图象不可能是( )A、
的图象一定经过点( ) A、(3,5) B、(-2,3) C、(2,7) D、(4,10)4. y=kx+(k-3)的图象不可能是( )A、 B、
B、 C、
C、 D、
D、 5. 直线 经过点 ,且 ,则b的值是( )A、 B、4 C、 D、86. 已知一次函数y=kx+b的图象如图,则k、b的符号是( )
5. 直线 经过点 ,且 ,则b的值是( )A、 B、4 C、 D、86. 已知一次函数y=kx+b的图象如图,则k、b的符号是( ) A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<07. 对于一次函数 y =kx + b (k, b 为常数),下表中给出几组自变量及其对应的函数值,
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<07. 对于一次函数 y =kx + b (k, b 为常数),下表中给出几组自变量及其对应的函数值,x
-1
0
1
3
y
7
5
2
-1
其中恰好有一个函数值计算有误,则这个错误的函数值是( )
A、-1 B、2 C、5 D、78. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( ) A、 B、 C、 D、9. 一次函数 与正比例函数 、 常数,且 ,在同一坐标系中的大致图象是( )A、
A、 B、 C、 D、9. 一次函数 与正比例函数 、 常数,且 ,在同一坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,直线y=-x+4分别与x轴,y轴交于A,B两点.从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )
10. 如图,直线y=-x+4分别与x轴,y轴交于A,B两点.从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( ) A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)
A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)二、填空题
-
11. 如图,过A点的一次函数图象与正比例函数y=2x的图象相交于点B , 则这个一次函数的表达式是 .
 12. 如果正比例函数 的图像经过原点和第一、第三象限,那么k的取值范围是 .13. 如图所示的图像反映的过程是:甲乙两人同时从 地出发,以各自的速度匀速向 地行驶,甲先到 地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为 , 表示甲乙两人相距的距离, 表示乙行驶的时间.现有以下 个结论:① 、 两地相距 ;②点 的坐标为 ;③甲去时的速度为 ;④甲返回的速度是 .以上 个结论中正确的是.
12. 如果正比例函数 的图像经过原点和第一、第三象限,那么k的取值范围是 .13. 如图所示的图像反映的过程是:甲乙两人同时从 地出发,以各自的速度匀速向 地行驶,甲先到 地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为 , 表示甲乙两人相距的距离, 表示乙行驶的时间.现有以下 个结论:① 、 两地相距 ;②点 的坐标为 ;③甲去时的速度为 ;④甲返回的速度是 .以上 个结论中正确的是. 14. 如图,在坐标系中,一次函数 与一次函数 的图像交于点 ,则关于 的不等式 的解集是.
14. 如图,在坐标系中,一次函数 与一次函数 的图像交于点 ,则关于 的不等式 的解集是.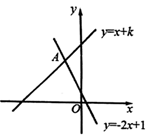 15. 如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC所在直线的函数表达式是y=2x+4,若保持AC的长不变,当点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动,则在滑动过程中,点B与原点O的最大距离是。
15. 如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC所在直线的函数表达式是y=2x+4,若保持AC的长不变,当点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动,则在滑动过程中,点B与原点O的最大距离是。 16. 如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4 , 0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
16. 如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4 , 0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
三、解答题
-
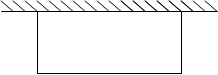
17. 已知:一次函数的图象与直线y=﹣2x+1平行,且过点(3,2),求此一次函数的解析式.18. 一次函数y=kx+b中(k、b为常数,k≠0),若-3≤x≤2,则-1≤y≤9,求一次函数的解析式.19. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围.
 20. 我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:
20. 我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:品种
购买价(元/棵)
成活率
甲
20
90%
乙
32
95%
设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1)、设y与x之间的函数关系式,并写出自变量x的取值范围;
(2)、承包商要获得不低于中标价16%的利润,应如何选购树苗?(3)、政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?21. 如图,在平面直角坐标系中,点F的坐标为(0,10).点E的坐标为(20,0),直线l1经过点F和点E,直线l1与直线l2、y= x相交于点P. (1)、求直线l1的表达式和点P的坐标;(2)、矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒 个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
(1)、求直线l1的表达式和点P的坐标;(2)、矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒 个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线l1或l2上,请直接写出此时t的值;
②若矩形ABCD在移动的过程中,直线CD交直线l1于点N,交直线l2于点M.当△PMN的面积等于18时,请直接写出此时t的值.
22. 我县为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题: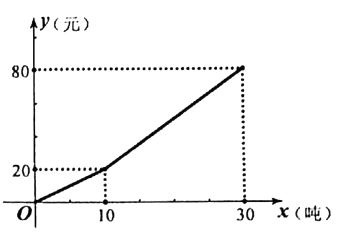 (1)、当用水量不超过10吨时,每吨水收费多少元?(2)、当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;(3)、某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。
(1)、当用水量不超过10吨时,每吨水收费多少元?(2)、当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;(3)、某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。