人教版数学八年级下册第十八章 平行四边形测试卷

试卷更新日期：2020-07-19 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 如图，在学习“四边形”一章时，小明的书上有一图因不小心被滴上墨水，看不清所印的字，请问被墨迹遮盖了的文字应是（    ）

    A、四边形 B、梯形 C、矩形 D、菱形

    查看试题解析

  • 2. 如图，Rt△ABC中，∠C=90°，AC=8，AB=10，D、E分别为AC、AB中点，连接DE，则DE长为（    ）

    A、4 B、3 C、8 D、5

    查看试题解析

  • 3. 已知四边形ABCD是平行四边形，下列结论中错误的是（  ）
    A、当 AB=BC 时，它是菱形 B、当 AC⊥BD 时，它是菱形 C、当 ∠ABC=90° 时，它是矩形 D、当 AC=BD 时，它是正方形

    查看试题解析

  • 4. 如图，平行四边形ABCD的对角线交于点E，已知AB=5cm，△ABE的周长比△BEC的周长小3cm，则AD的长度为（ ）

    A、8cm B、5cm C、3cm D、2cm

    查看试题解析

  • 5. 如图，在四边形 ABCD 中， E 是 BC 边的中点，连接 DE 并延长，交 AB 的延长线于点 F ， AB=BF ．添加一个条件使四边形 ABCD 是平行四边形，你认为下面四个条件中可选择的是（    ）

    ​​

    A、AD=BC B、CD=BF C、∠A=∠C D、∠F=∠CDF

    查看试题解析

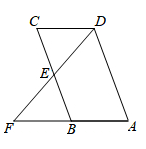  • 6. 如图，正方形ABCD的面积为8，菱形AECF的面积为4，则EF的长是（    ）

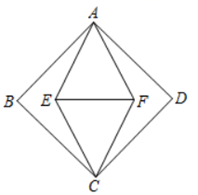    A、4 B、5 C、2 D、1

    查看试题解析

  • 7. 如图，一根竹竿AB，斜靠在竖直的墙上，P是AB中点，A'B'表示竹竿AB端沿墙上、下滑动过程中的某个位置，则在竹竿AB滑动过程中OP（ ）

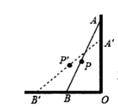    A、下滑时，OP增大 B、上升时，OP减小 C、无论怎样滑动，OP不变 D、只要滑动，OP就变化

    查看试题解析

  • 8. 以下四个条件中可以判定四边形是平行四边形的有（ ）

    ①两组对边分别平行；

    ②两组对边分别相等；

    ③有一组对边平行且相等；

    ④对角线相等．

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 9. 如图，在平行四边形ABCD中，∠B＜90°，BC＞AB．作AE⊥BC于点E，AF⊥CD于点F，记∠EAF的度数为α，AE＝a，AF＝b．则以下选项错误的是（ ）

    A、∠D的度数为α B、a∶b＝CD∶BC C、若α＝60°，则平行四边形ABCD的周长为 433(a+b) D、若α＝60°，则四边形AECF的面积为平行四边形ABCD面积的一半

    查看试题解析

  • 10.

    如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论①AE=BF；②AE⊥BF；③ AO=OE；④ S△AOB=S四边形DEOF 中，错误的有（      ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 11. 在平行四边形ABCD中，若∠A+∠C=140°，则∠B= ．

    查看试题解析

  • 12. Rt△ABC中∠ABC=90°，斜边AC=10cm，D为斜边上的中点，斜边上的中线BD=.

    查看试题解析

  • 13. 如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=12，则HE等于.

    查看试题解析

  • 14. 如图，在▱ABCD中，以点A为圆心，以任意长为半径画圆弧，分别交边AD、AB于点M、N ， 再分别以点M、N为圆心，以大于 12MN 长为半径画圆弧，两弧交于点P ， 作射线AP交边CD于点E ， 过点E作EF∥AD交AB于点F ． 若AB=5，CE=2，则四边形ADEF的周长为 ．

    查看试题解析

  • 15. 如图所示，DE为 △ABC 的中位线，点F在DE上，且 ∠AFB=90° ，若 AB=4 ， BC=10 ，则 EF 的长为.

    查看试题解析

  • 16. 如图，点O是▱ABCD的对角线交点，AD＞AB，E、F是AB边上的点，且EF= 12 AB；G、H是BC边上的点，且GH= 13 BC，若S1 ， S2分别表示△EOF和△GOH的面积，则S1：S2= ．

    查看试题解析

  • 17. 如图，已知▱OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为 ．

    查看试题解析

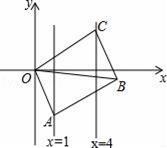
三、解答题

  • 18. 如图，在▱ABCD中，AE⊥BD于点E，BM⊥AC于点M，CN⊥BD于点N，DF⊥AC于点F.求证：EF∥MN.

    查看试题解析

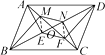  • 19. 如图，已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F，∠ADC的平分线DG交边AB于G.求证：AF=GB

    查看试题解析

  • 20. 已知：如图，四边形ABCD中，AC⊥BD ， E、F、G、H分别为AB、BC、CD 、DA的中点，判断EG与FH的数量关系并加以证明．

    查看试题解析

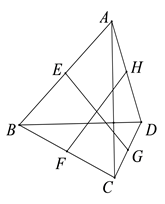  • 21. 已知：如图，平行四边形ABCD，对角线AC与BD相交于点E，点G为AD的中点，且AG＝AB、CG的延长线交BA的延长线于点F，连接FD.试探究当∠BCD＝▲°时，四边形ACDF是矩形，证明你的结论.

    查看试题解析

四、综合题

  • 22. 如图：在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB上一点，过点D作DE⊥BC，交直线MN于点E，垂足为F，连结CD，BE，

    (1)、当点D是AB的中点时，四边形BECD是什么特殊四边形？说明你的理由
    (2)、在（1）的条件下，当∠A=时四边形BECD是正方形．

    查看试题解析

  • 23. 如图，在等腰直角三角形ABC中， ∠ACB=90° ， AC=BC=4 ，D是AB的中点，E、F分别是AC、BC上的点（点E不与端点A、C重合），连接EF并取EF的中点O，连接DO并延长至点G，使 GO=OD ，连接DE、GE、GF.

    (1)、求证：四边形EDFG是平行四边形；
    (2)、若 AE=CF ，探究四边形EDFG的形状？
    (3)、在（2）的条件下，当E点在何处时，四边形EDFG的面积最小，并求出最小值.

    查看试题解析