人教版数学七年级下册第七章平面直角坐标系测试卷

试卷更新日期：2020-07-19 类型：单元试卷

进入出卷网下载

一、单选题

1. 点P（2，－3）在第四象限，则点P到x轴的距离是（）

A、2 B、3 C、-2 D、-3

查看试题解析
2. 课间操时，小华、小军和小刚的位置如图所示，如果小华的位置用(0，0)表示，小军的位置用(2，1)表示，那么小刚的位置可以表示为（）

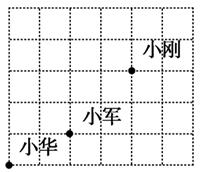A、(5，4) B、(4，5) C、(3，4) D、(4，3)

查看试题解析
3. 点C在轴的下方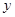，轴的右侧，距离轴3个单位长度，距离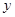轴5个单位长度，则点C的坐标为（）

A、（－3，5） B、（3，－5） C、（5，－3） D、（－5，3）

查看试题解析
4. 如图，学校相对于小明家的位置下列描述最准确的是（）

A、距离学校 $1200$ 米处 B、北偏东 $65 °$ 方向上的 $1200$ 米处 C、南偏西 $65 °$ 方向上的 $1200$ 米处 D、南偏西 $25 °$ 方向上的 $1200$ 米处

查看试题解析
5. 将点A(-2，3)沿x轴向左平移3个单位长度，再沿y轴向上平移4个单位长度后得到的点A'的坐标为（）

A、(1，7) B、(1，-1) C、(-5，-1) D、(-5，7)

查看试题解析
6. 如图，在平面直角坐标系中，点根据这个规律，探究可得点 $A_{1} (1 ， 2)$ ， $A_{2} (2 ， 0)$ ， $A_{3} (3 ， - 2)$ ， $A_{4} (4 ， 0)$ ......根据这个规律，探究可得点 $A_{2020}$ 的坐标是（）．

A、（2020，0） B、（2020，2） C、（2020，-2） D、（2021，0）

查看试题解析
7. 在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：①f（a，b）=（-a，b），如f（1，2）=（-1，2）；②g（a，b）=（b，a），如g（1，2）=（2，1）；③h（a，b）=（-a，-b），如h（1，2）=（-1，-2）；按照以上变换有：g（h（f（1，2）））=g（h（-1，2））=g（1，-2）=（-2，1），那么h（f（g（3，-4）））等于（）

A、（4，-3） B、（-4，3） C、（-4，-3） D、（4，3）

查看试题解析
8. 如图，点 $A ， B$ 的坐标分别为 $(1 ， 2)$ 、 $(4 ， 0)$ ，将 $Δ A O B$ 沿 $x$ 轴向右平移，得到三角形 $C D E$ ，已知 $D B = 1$ ，则点 $C$ 的坐标为（）

A、 $(5 ， 2)$ B、 $(4 ， 2)$ C、 $(5 ， 3)$ D、 $(4 ， 3)$

查看试题解析
9. 如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为(1，0)、(2，0)、(2，1)、(1，1)、(1，2)、(2，2)、……，根据这个规律，第2019个点的坐标为（）

A、(45，10) B、(45，6) C、(45，22) D、(45，0)

查看试题解析
10. 如图，点A₁（1，1），点A₁向上平移1个单位，再向右平移2个单位，得到点A₂；点A₂向上平移2个单位，再向右平移4个单位，得到点A₃；点A₃向上平移4个单位，再向右平移8个单位，得到点A₄ ， ……，按这个规律平移得到点A_n ，则点A_n的横坐标为（　　）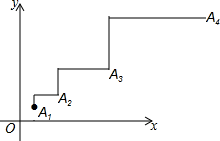

A、2ⁿ B、2^n-1 C、2ⁿ-1 D、2ⁿ+1

查看试题解析

二、填空题

11. 点P(3，-4)到x轴的距离是．

查看试题解析
12. 已知坐标平面内一动点P(1，2)，先沿x轴的正方向平移3个单位，再沿y轴的负半轴方向平移3个单位后停止，此时P的坐标是

查看试题解析
13. 如图，在围棋盘上有三枚棋子，如果黑棋①的位置用坐标表示为 $(0 ， - 1)$ ，黑棋②的位置用坐标表示为 $(- 3 ， 0)$ ，则白棋③的位置用坐标表示为.

查看试题解析
14. 若点A(m+3，1-m)在y轴上，则点A的坐标为。

查看试题解析
15. 已知点A（1，0），B（2，2），点P在y轴上，且△PAB的面积为5，则点P的坐标是．

查看试题解析
16. 如图，若在中国象棋盘上建立平面直角坐标系，使“帅”位于点，“马”位于点，则“兵”位于点.

查看试题解析
17. 如图，在方格纸上，△ABC向右平移格后得到△A₁B₁C₁.

查看试题解析
18. 如图，在直角坐标系中，右边的蝴蝶是由左边的蝴蝶飞过去以后得到的，左图案中左右翅尖的坐标分别是(－4，2)、(－`2，2)，右图案中左翅尖的坐标是(3，4)，则右图案中右翅尖的坐标是.

查看试题解析
19. 如图，已知A₁（1，0），A₂（1，﹣1），A₃（﹣1，﹣1），A₄（﹣1，1），A₅（2，1），…，则点A₂₀的坐标是．

查看试题解析
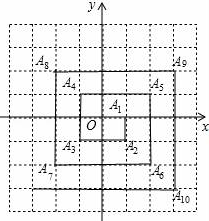20. 如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点 $A_{1} (0 ， 1)$ ， $A_{2} (1 ， 1)$ ， $A_{3} (1 ， 0)$ ， $A_{4} (2 ， 0)$ ， $\dots$ 那么点 $A_{2018}$ 的坐标为.

查看试题解析

三、解答题

21. 古城黄州以其名胜古迹吸引了不少游客，从地图上看，较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处，黄冈中学在市政府以东1km处，宝塔公园在市政府以东3km处，鄂黄大桥在市政府以东7km再往北8km处，遗爱湖在市政府以东4km再往北4km处，博物馆在市政府以北2km再往西1km处．请画图表示出这六个景点的位置，并用坐标表示出来．

查看试题解析
22. 已知四边形AOCD是放置在平面直角坐标系内的梯形，其中O是坐标原点，点A，C，D的坐标分别为（0，8），（5，0），（3，8）.若点P在梯形内，且△PAD的面积等于△POC的面积，△PAO的面积等于△PCD的面积. 求点P的坐标.

查看试题解析
23. 如图，将△ABC中向右平移4个单位得到△A′B′C′．
①写出A、B、C的坐标；
②画出△A′B′C′；
③求△ABC的面积．

查看试题解析
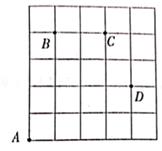
24. 阅读与理解：
如图，一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行．若我们规定：在如图网格中，向上(或向右)爬行记为“+”，向下(或向左)爬行记为“-”，并且第一个数表示左右方向，第二个数表示上下方向。

例如：从A到B记为：A→B(+1，+4)，

从D到C记为：D→C(-1，+2)。

思考与应用：

(1)、图中A→C( ， )；
B→C( ， )；

D→A( ， )。

(2)、若甲虫从A到P的行走路线依次为：(+3，+2)→(+1，+3)→(+1，-2)，请在图中标出P的位置。

(3)、若甲虫的行走路线为A一(+1，+4)→(+2，0)→(+1，-2)-(-4，-2)，请计算该甲虫走过的总路程。

查看试题解析

四、综合题

25. 如图 1，在平面直角坐标系中，已知点A(a，0)，B(b，0)，C(2，7)，连接 AC，交y轴于 D，且 $a = \sqrt[3]{- 125}$ ， ${(\sqrt{b})}^{2} = 5$ .

(1)、求点D的坐标.

(2)、如图 2，y轴上是否存在一点P，使得△ACP的面积与△ABC的面积相等？若存在，求点P的坐标，若不存在，说明理由.

(3)、如图 3，若 Q(m，n)是 x轴上方一点，且 $△ Q B C$ 的面积为20，试说明：7m＋3n是否为定值，若为定值，请求出其值，若不是，请说明理由.

查看试题解析