人教版数学七年级下册第六章实数测试卷

试卷更新日期：2020-07-19 类型：单元试卷

进入出卷网下载

一、单选题

1. 在 $\frac{1}{3}$ ， $\sqrt{5}$ ， $π - 3.14$ ， $\sqrt{81}$ ，中，无理数有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 如果一个实数的平方根与它的立方根相等，则这个数是（）

A、0 B、正整数 C、0或1 D、1

查看试题解析
3. 计算 $| \sqrt[3]{27} | + | - \sqrt{16} | + \sqrt{4} - \sqrt[3]{8}$ 的值是（　　）

A、1 B、 $\pm 1$ C、2 D、7

查看试题解析
4. 下列整数中、与10- $\sqrt{13}$ 最接近的是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 已知a－1=b+1=c－2=d－3，则a、b、c、d这四个数中最小的是（）

A、a B、b C、c D、d

查看试题解析
6. 若 $k < \sqrt{90} < k + 1 (k$ 是整数），则 $k = ($ 　　 $)$

A、9 B、8 C、7 D、6

查看试题解析
7. 如果3a-21和2a+1是正实数m的两个不同的平方根，那么 $\sqrt{m}$ 的值为（　　）

A、2 B、3 C、4 D、9

查看试题解析
8. 下列说法错误的是（）

A、 $\sqrt{25}$ 的平方根是 $\pm \sqrt{5}$ B、 ${(- 4)}^{2}$ 的算术平方根是4 C、0的立方根是0 D、64的立方根是 $\pm 4$

查看试题解析
9. 如图所示，数轴上表示2， $\sqrt{5}$ 的对应点分别为C，B，点C是AB的中点，则点A表示的数是（）

A、 $1$ B、 $2 - \sqrt{5}$ C、 $4 - \sqrt{5}$ D、 $\sqrt{5} - 2$

查看试题解析
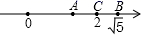10. 关于 $\sqrt[3]{12}$ 的叙述，错误的是（）

A、 $\sqrt[3]{12}$ 表示12的立方根 B、在数轴上可以找到表示 $\sqrt[3]{12}$ 的点 C、 $\sqrt[3]{12}$ 是有理数 D、体积为12的正方体的棱长是 $\sqrt[3]{12}$

查看试题解析

二、填空题

11. 下列实数中，无理数有.（填序号）
①-2，② $\sqrt{3}$ ，③ $\frac{π}{2}$ ，④ $\sqrt{144}$ ，⑤ $- \frac{\sqrt{8}}{2}$ ，⑥ $\frac{22}{7}$ ，⑦ $\sqrt[3]{- 27}$ ，⑧1.101001.

查看试题解析
12. 计算：

(1)、 $\sqrt{25}$ ；

(2)、 $\sqrt[3]{- 27} =$ .

查看试题解析
13. $\sqrt{81}$ 的算术平方根是， $\sqrt[3]{1 + 2 \frac{3}{8}}$ = ．

查看试题解析
14. 若 $\sqrt[3]{0.3670}$ ＝0.7160， $\sqrt[3]{3.670}$ ＝1.542，则 $\sqrt[3]{367}$ ＝， $\sqrt[3]{- 0.003670}$ ＝．

查看试题解析
15. 一个正数的平方根是 $2 x - 1$ 和 $2 - x$ ，则 $\sqrt{13 - 3 x}$ 的算术平方根为.

查看试题解析
16. 已有数2、3、x，这三个数中，一个数是另外两个数的乘积的一个平方根,那么x可能是.

查看试题解析
17. $\sqrt{6.5}$ 的整数部分为，估计 $\sqrt{6.5}$ ≈（结果精确到0.1）．

查看试题解析
18. 规定用符号[m]表示一个实数m的整数部分，例如[ $\frac{2}{3}$ ]＝0，[3.14]＝3．按此规定 $[- \sqrt{17} + 1]$ 的值为．

查看试题解析

三、解答题

19. 把下列各数分别填在相应的集合中：
$\frac{22}{7}$ ，3.1415926， $\sqrt{5}$ ， $- 0.8$ ， $\sqrt[3]{2}$ ， $- \sqrt{7}$ ， $\sqrt{36}$ ， $\frac{π}{3}$ .

查看试题解析
20. 如图，将数轴上标有字母的各点与下列实数对应起来，请在答题卡上填写对应的实数：- $\frac{1}{2}$ ，π，0， $\sqrt{2}$ ，2，- $\sqrt{3}$ ．

查看试题解析
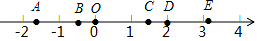21. 已知A= $\sqrt[4 a - b - 3]{a + 2}$ 是 $a + 2$ 的算术平方根，B = $\sqrt[3 a + 2 b - 9]{2 - b}$ 是 $2 - b$ 的立方根.求6A+3B的平方根.

查看试题解析
22. “比差法”是数学中常用的比较两个数大小的方法，即： ${\begin{matrix} \begin{array}{l} a - b > 0 ，则 a > b \\ a - b = 0, 则 a = b \end{array} \\ a - b < 0, 则 a < b \end{matrix}$ ；
例如：比较 $\sqrt{19} - 2$ 与2的大小

∵ $\sqrt{19} - 2 - 2 = \sqrt{19} - 4$ 又∵ $\sqrt{16} < \sqrt{19} < \sqrt{25}$ 则 $4 < \sqrt{19} < 5$

∴ $\sqrt{19} - 2 - 2 = \sqrt{19} - 4 > 0$

∴ $\sqrt{19} - 2 > 2$

请根据上述方法解答以下问题：比较 $2 - \sqrt{23}$ 与 $- 3$ 的大小.

查看试题解析
23. 阅读下面的文字，解答问题：大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2}$ -1来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分。

又例如：

∵ $\sqrt{4}$ < $\sqrt{7}$ < $\sqrt{9}$ ，即2< $\sqrt{7}$ <3，

∴ $\sqrt{7}$ 的整数部分为2，小数部分为( $\sqrt{7}$ -2)．

请解答：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是。

(2)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求a+b- $\sqrt{5}$ 的值；

(3)、已知：10+ $\sqrt{3}$ =x+y，其中x是整数，且0<y<1，求x-y的相反数。

查看试题解析

四、综合题

24. 操作探究：已知在纸面上有一数轴（如图所示）

(1)、折叠纸面，使表示的点1与﹣1重合，则﹣2表示的点与表示的点重合；

(2)、折叠纸面，使﹣1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数表示的点重合；
② $\sqrt{3}$ 表示的点与数表示的点重合；
③若数轴上A、B两点之间距离为9（A在B的左侧），且A、B两点经折叠后重合，此时点A表示的数是、点B表示的数是

(3)、已知在数轴上点A表示的数是a，点A移动4个单位，此时点A表示的数和a是互为相反数，求a的值.

查看试题解析