人教版数学七年级下册第五章相交线和平行线测试卷
试卷更新日期：2020-07-19 类型：单元试卷
一、单选题
-
1. 如图，一个含30°角的直角三角板的两个顶点放在一个长方形的对边上，若∠1=20°，那么∠2的度数是（ ）
A、100° B、105° C、110° D、120°2. 下列命题中，正确的是（ ）A、对顶角相等 B、同位角相等 C、内错角相等 D、同旁内角互补3. 将点A（-1，2）向右平移3个单位长度，再向下平移5个单位长度，则平移后点的坐标是（ ）A、（2，3） B、（-2，-3） C、（2，-3） D、（-2，3）4. 如图，点E在AD的延长线上，下列条件中能判断BC∥AD的是（ ）
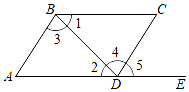A、∠1＝∠2 B、∠A＝∠5 C、∠A+∠ADC＝180° D、∠3＝∠45. 如图，将 沿射线 方向平移得到 ，若 ，则线段 的长是（ ）
A、4 B、5 C、6 D、86. 如图，直线a∥b，直线AB⊥AC，若∠1＝50°，则∠2的度数为（ ）
A、50° B、45° C、30° D、40°7. 如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（ ）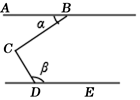
A、∠α+∠β＝95° B、∠β﹣∠α＝95° C、∠α+∠β＝85° D、∠β﹣∠α＝85°8. 如图，已知∠1+∠2=180°，∠AEF=∠HGN，则图中平行的直线有（ ）
A、0 对 B、1对 C、2对 D、3对9. 已知：如图，点E，F分别在直线AB，CD上，点G，H在两直线之间，线段EF与GH相交于点O，且有∠AEF+∠CFE=180°，∠AEF-∠1=∠2，则在图中相等的角共有（ ）
A、5对 B、6对 C、7对 D、8对10. 如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（ ）
①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 如图，已知AB∥CD，∠1=130°，则∠2=.
12. 如图，直径为2cm的⊙O1平移3cm到⊙O2 ， 则图中阴影部分的面积为cm2.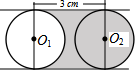
13. 将“对顶角相等”改写为“如果...那么...”的形式，可写为.14. 如图，在铁路旁有一李庄，现要建一火车站，为了使李庄人乘车最方便，在铁路线上选一点来建火车站，应建在点.
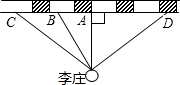15. 如图， ，一副三角尺按如图所示放置，∠AEG=20度，则 为 度.
16. 若∠A 的两边与∠B 的两边分别平行，且∠A－∠B＝40°，则∠A＝度.17. 如图，已知AB∥CD，∠B=25°，∠D=45°，则∠E=度．
18. 如图，是一块从一个边长为25cm的正方形BCDM材料中剪出的垫片，经测得FG＝8cm，则这个剪出的图形的周长是cm．
19. 已知 和 的两边分别平行，若 ，则 .20. 如图，∠AOB的两边OA、OB均为平面反光镜，∠AOB＝40°，在射线OB上有一点P ， 从点P点射出的一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是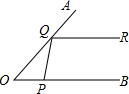
三、解答题
-
21. 如图，已知AB∥CD，∠1 = (4x-25)°，∠2 = (85-x)°，求∠1的度数.
22. 如图，已知AD⊥BC，FG⊥BC，垂足分别为D、G．且∠1 =∠2，猜想：∠BED与∠BAC有怎样的关系?说明理由．
23. 如图，EF∥AD ， AD∥BC ， CE平分∠BCF ， ∠DAC＝120°，∠ACF＝20°，求∠FEC的度数．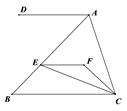
24. 如图， ∠ABE+ ∠DEB=180°， ∠1= ∠2．求证： ∠F= ∠G．
四、综合题
-
25. 已知，直线AB∥CD，E为AB、CD间的一点，连接EA、EC．
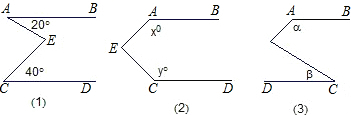(1)、如图①，若∠A=20°，∠C=40°，则∠AEC=°．(2)、如图②，若∠A=x°，∠C=y°，则∠AEC=°．(3)、如图③，若∠A=α，∠C=β，则α，β与∠AEC之间有何等量关系．并简要说明．26. 如图1，AD∥BC，∠BAD的平分线交BC于点G，∠BCD＝90°．
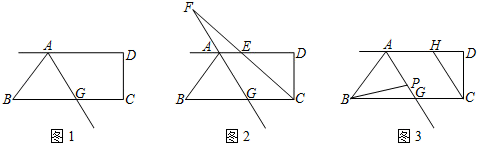(1)、求证：∠BAG＝∠BGA；(2)、如图2，若∠ABG＝50°，∠BCD的平分线交AD于点E、交射线GA于点F．求∠AFC的度数；(3)、如图3，线段AG上有一点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，请直接写出 的值．