2020年暑期衔接训练人教版数学八年级下册：第7讲 正方形
试卷更新日期：2020-07-19 类型：复习试卷
一、单选题
-
1. 顺次连接四边形各边中点所构成的四边形是正方形，则原四边形可能是（ ）A、平行四边形 B、矩形 C、菱形 D、正方形2. 下列说法不能判断是正方形的是（ ）A、对角线互相垂直且相等的平行四边形 B、对角线互相垂直的矩形 C、对角线相等的菱形 D、对角线互相垂直平分的四边形3. 如图，四边形ABCD中，AC、BD交于点O，则根据下列条件能判定它是正方形的是（ ）
A、∠DAB=90°且AD=BC B、AB=BC且AC=BD C、∠DAB=90°且AC⊥BD D、AC⊥BD且AO=BO=CO=DO4. 如图，在正方形 中， 是 上的一点，且 ，则 的度数是（ ）
A、 B、 C、 D、5. 如图，把一个长方形纸片对折两次，然后沿图中虚线剪下一个角，为了得到一个正方形，剪口与折痕所成的角的大小等于（ ）
A、30° B、45° C、60° D、90°6. 如图，四边形ABCD是正方形，直线L1、L2、L3 ， 若L1与L2的距离为5，L2与L3的距离7，则正方形ABCD的面积等于（ ）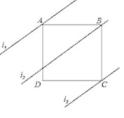
A、70 B、74 C、144 D、1487. 如图，正方形ABCD中，E、F是对角线AC上两点，连接BE、BF、DE、DF ， 则添加下列条件①∠ABE＝∠CBF；②AE＝CF；③AB＝AF；④BE＝BF ． 可以判定四边形BEDF是菱形的条件有（ ）
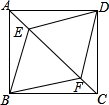A、1个 B、2个 C、3个 D、4个8. 如图，已知正方形ABCD的边长为4，P是对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接AP，EF．给出下列结论：①PD＝ EC；②四边形PECF的周长为8；③△APD一定是等腰三角形；④AP＝EF；⑤EF的最小值为2 ；⑥AP⊥EF．其中正确结论的序号为（ ）
A、①②④⑤⑥ B、①②④⑤ C、②④⑤ D、②④⑤⑥9. 如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE＝22.5°，EF⊥AB，垂足为F，则EF的长为（ ）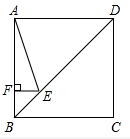
A、1 B、 C、4－2 D、3 －410.如图，E是边长为4的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BR于点R，则PQ+PR的值是（ ）
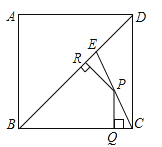A、2 B、2 C、2 D、二、填空题
-
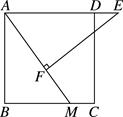
11. 已知正方形ABCD在直角坐标系中，A(2，2)，B(4，2)．那么C点的坐标为 ．12. 如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为
13.如图，在Rt△ABC中，∠C＝90°，DE垂直平分AC ， DF⊥BC ， 当△ABC满足条件时，四边形DECF是正方形．（要求：①不再添加任何辅助线，②只需填一个符合要求的条件）
14. 如图，正方形ABCD的对角线长为8，E为AB上一点，若EF⊥AC于点F，EG⊥BD于点G，则EF+EG＝.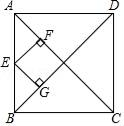
15. 如图，正方形 的边长为4，则图中的阴影部分面积为.
16. 将2016个边长为1的正方形按照如图所示方式摆放，O1 ， O2 ， O3 ， O4 ， O5 ， …是正方形对角线的交点，那么阴影部分面积之和等于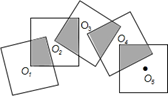
17. 如图，点E为正方形ABCD外一点，且ED=CD ， 连接AE ， 交BD于点F ． 若∠CDE=40°，则∠DFC的度数为
三、解答题
-
18. 如图，四边形ABCD是正方形，M为BC上的点，连接AM，延长AD至点E，使得AE＝AM，过点E作EF⊥AM，垂足为F.
求证：AB＝EF.
19. 如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长交BC于点G．连接AG．求证：△ABG≌△AFG．
20. 已知：如图，在Rt△ABC中，∠C=90°，∠BAC、∠ABC的平分线相交于点D，DE⊥BC，DF⊥AC，垂足分别为E、F．求证：四边形CEDF是正方形．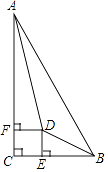
四、综合题
-
21. △ABC中，点O是AC上一动点，过点O作直线MN∥BC，若MN交∠BCA的平分线于点E，交∠DCA的平分线于点F，连接AE、AF.
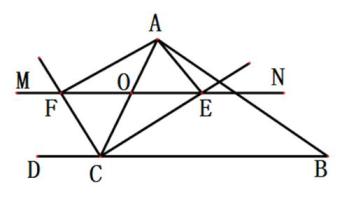(1)、说明：OE＝OF(2)、当点O运动到AC中点处时，求证：四边形AECF是矩形；(3)、在(2)的条件下，当△ABC满足什么条件时，四边形AECF为正方形，并加以证明.22. 如图，△ABC是等腰直角三角形，∠A=90°，点P，Q分别是AB， AC上的一动点，且满足BP=AQ，D是BC的中点.
(1)、求证：△PDQ是等腰直角三角形.(2)、当点P运动到什么位置时，四边形APDQ是正方形，并说明理由.
