2020年暑期衔接训练人教版数学八年级下册：第6讲 菱形
试卷更新日期：2020-07-19 类型：复习试卷
一、单选题
-
1. 已知菱形 的对角线 的长分别为6，8，则菱形的周长为（ ）A、10 B、20 C、24 D、402. 已知菱形的两条对角线长分别是6和8，则菱形的面积是（ ）A、48 B、30 C、24 D、203. 菱形的对角线不具备的性质是（ ）A、对角线互相平分 B、对角线一定相等 C、对角线一定垂直 D、对角线平分一组对角4. 如图，菱形 中， ，则 （ ）
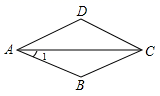A、 B、 C、 D、5. 如图，要使平行四边形ABCD成为菱形，添加一个条件不正确的是（ ）
A、AC⊥BD B、AB=AD C、AC=BD D、AC平分∠BAD6. 如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（ ）
A、75° B、65° C、55° D、50°7. 如图，四边形ABCD是菱形，对角线AC＝8，DB＝6，DH⊥AB于点H，则DH的长为( )
A、4.8cm B、5cm C、9.6cm D、10cm8. 如图，菱形ABCD的对角线AC、BD相交于点O ， 过点C作CE⊥AD于点E ， 连接OE ， 若OB＝8，S菱形ABCD＝96，则OE的长为（ ）
A、2 B、2 C、6 D、89. 如图，在菱形 中，E ， F分别是 的中点，若∠B=50°，则∠AFE的度数为（ ）
A、50° B、60° C、65° D、70°10. 如图，菱形ABCD的周长为40cm，对角线AC、BD相交于点O，DE⊥AB，垂足为E，DE：AB=4：5，则下列结论：①DE=8cm；②BE=4cm；③BD=4 cm；④AC=8 cm；⑤S菱形ABCD=80cm，正确的有（ ）
A、①②④⑤ B、①②③④ C、①③④⑤ D、①②③④⑤11. 如图，在Rt△ABC中，∠B=90°，AC=120cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒．过点D作DF⊥BC于点F，连接DE，EF．当四边形AEFD是菱形时，t的值为（ ）
A、20秒 B、18秒 C、12秒 D、6秒二、填空题
-
12. 若菱形的面积为24，一条对角线长为8，则另一条对角线长为 ， 边长为.13. 两个全等菱形如图所示摆放在一起，其中 和 分别在同一条直线上，若较短的对角线长为10，点 与点 的距离是24，则此菱形边长为.
14. 如图，在菱形ABCD中，若AC＝24 cm，BD＝10 cm，则菱形ABCD的高为cm.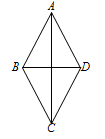
15. 如图，在菱形ABCD中，∠BAD=70°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，则∠CDF=°.
16. 如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2015次，点B的落点依次为B1 ， B2 ， B3 ， …，则B2015的坐标为 ．
三、解答题
-
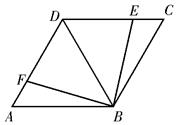
17. 如图，用3个全等的菱形构成活动衣帽架，顶点A、E、F、C、G、H是上、下两排挂钩，根据需要可以改变挂钩之间的距离（比如AC两点可以自由上下活动），若菱形的边长为13厘米，要使两排挂钩之间的距离为24厘米，并在点B、M处固定，则B、M之间的距离是多少？
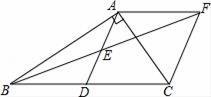
18. 如图，在△ABC中，∠BAC＝90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF，求证：四边形ADCF是菱形．
