2020年暑期衔接训练人教版数学八年级下册：第5讲 矩形
试卷更新日期：2020-07-19 类型：复习试卷
一、单选题
-
1. 如图，在长方形钟面示意图中，时钟的中心在长方形对角线的交点上，长方形宽为 40cm ， 钟面数字 2 在长方形的顶点处，则长方形的长为（ ）cm
A、80 B、60 C、50 D、402. 下列条件中，不能判定平行四边形ABCD为矩形的是（ ）A、∠A＝∠C B、∠A＝∠B C、AC＝BD D、AB⊥BC3. 如图，矩形ABCD中，∠AOB=60°，AB=2，则AC的长为（ ）
A、4 B、2 C、 D、4. 在矩形ABCD中，AB=3，BC=4，E是BC上一点，且与B、C不重合，若AE是整数，则AE等于（ ）
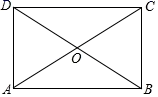
A、3 B、4 C、5 D、65. 如图，顺次连接四边形ABCD各边的中点的四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）
A、AB∥DC B、AC=BD C、AC⊥BD D、AB=CD6. 如图，点O是矩形ABCD的对角线AC的中点，M是CD边的中点.若AB=8，OM=3，则线段OB的长为（ ）
A、5 B、6 C、8 D、107. 如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是（ ）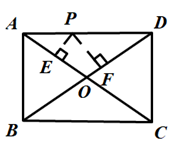
A、 B、 C、 D、无法确定8. 如图，四边形ABCD为平行四边形，延长AD到点E，使DE＝AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（ ）
A、AB＝BE B、BE⊥DC C、∠ADB＝90° D、CE⊥DE9. 如图，点 是矩形 的对角线 的中点， 是 边的中点，若 ，则 的长为（ ）
A、5 B、6 C、8 D、1010. 如图，矩形ABCD的面积为1cm2 ， 对角线交于点O；以AB、AO为邻边作平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边作平行四边形AO1C2B…；依此类推，则平行四边形AO2014C2015B的面积为（ ）
A、 B、 C、 D、二、填空题
-
11. 在四边形ABCD中，对角线AC ， BD交于点O且AC ， BD互相平分，若添加一个条件使得四边形ABCD是矩形，则这个条件可以是(填写一个即可)．
12. 如图，矩形ABCD中，点E，F分别是AB，CD的中点，连接DE和BF，分别取DE，BF的中点M，N，连接AM， CN，MN，若AB=2，BC=3，则图中阴影部分的面积为.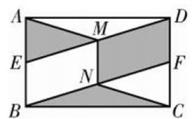
13. 如图，矩形ABCD的对角线AC与BD相交点O ， ，P、Q分别为AO、AD的中点，则PQ的长度为 ．
14. 如图，△ABC中，∠B=90°，AB=4， BC=3，点D是AC上的任意一点，过点D作DE⊥AB于点E，DF⊥BC于点F，连接EF，则EF的最小值是。
15. 如图，矩形ABCD中，AC、BD交于点O，∠AOB=60°，DE平分∠ADC交BC于点E，连接OE，则∠COE= ．
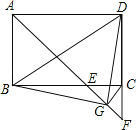
16.如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：
①BE=CD；
②∠DGF=135°；
③∠ABG+∠ADG=180°；
④若= ， 则3S△BDG=13S△DGF ．
其中正确的结论是 （写所有正确结论的序号）.
三、解答题
-
17. 如图，矩形 中， 、 的平分线 、 分别交边 、 于点 、 。求证；四边形 是平行四边形。
18. 如图，在△ABC中，AB=AC，D为BC边的中点，以AB、BD为邻边作▱ABDE，连接AD，EC．求证：四边形ADCE是矩形．
