2012年辽宁省铁岭市中考数学试卷
试卷更新日期:2016-05-13 类型:中考真卷
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 3的相反数是( )A、3 B、﹣3 C、 D、﹣2. 下列图形中,不是中心对称的是( )A、
 B、
B、 C、
C、 D、
D、 3. 计算(﹣2a3)2的结果是( )
3. 计算(﹣2a3)2的结果是( )
A、2a5 B、4a5 C、﹣2a6 D、4a64.如图,桌面上是由长方体的茶叶盒与圆柱体的茶叶盒组成的一个立体图形,其左视图是( )
 A、
A、 B、
B、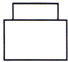 C、
C、 D、
D、 5. 为了解长城小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表:
5. 为了解长城小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表:锻炼时间(时)
3
4
5
6
7
人数(人)
6
13
14
5
2
这40名居民一周体育锻炼时间的中位数是( )
A、4小时 B、4.5小时 C、5小时 D、5.5小时6.在如图所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为( )
 A、 B、 C、 D、7.
A、 B、 C、 D、7.如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是( )
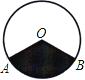 A、1 B、 C、 D、28.
A、1 B、 C、 D、28.矩形纸片ABCD中,AB=4,AD=8,将纸片沿EF折叠使点B与点D重合,折痕EF与BD相交于点O,则DF的长为( )
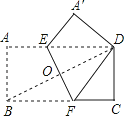 A、3 B、4 C、5 D、69.
A、3 B、4 C、5 D、69.如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
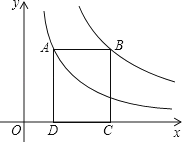 A、12 B、10 C、8 D、610.
A、12 B、10 C、8 D、610.如图,▱ABCD的边长为8,面积为32,四个全等的小平行四边形对称中心分别在▱ABCD的顶点上,它们的各边与▱ABCD的各边分别平行,且与▱ABCD相似.若小平行四边形的一边长为x,且0<x≤8,阴影部分的面积的和为y,则y与x之间的函数关系的大致图象是( )
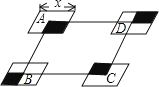 A、
A、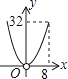 B、
B、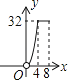 C、
C、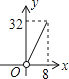 D、
D、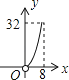
二、填空题(本题共8小题,每小题3分,共24分)
-
11. 2011年10月20日,为更好地服务我国367 000 000未成年人,在团中央书记处领导下,团中央网络影视中心开通面向全国未成年人的专属网站﹣﹣未来网.将367 000 000用科学记数法表示为 .12. 如果 +|y﹣2|=0,那么xy= .13.
如图,已知∠1=∠2,∠B=40°,则∠3= .
 14.
14.从﹣2、1、 这三个数中任取两个不同的数相乘,积是无理数的概率是 .
15. 某城市进行道路改造,若甲、乙两工程队合作施工20天可完成;若甲、乙两工程队合作施工5天后,乙工程队再单独施工45天可完成.求乙工程队单独完成此工程需要多少天?设乙工程队单独完成此工程需要x天,可列方程为 .16.如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行海里.
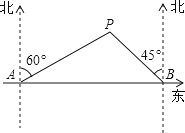 17.
17.如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为 .
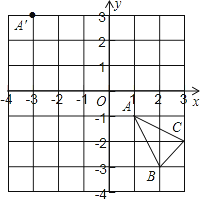 18.
18.如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2 , 以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为 .
三、解答题(第19题10分,第20题12分,共22分)
-
19. 先化简,再求值: ,其中x=3tan30°+1.20.
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.
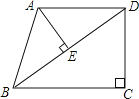 (1)、求证:△ABE∽△DBC;(2)、求线段AE的长.
(1)、求证:△ABE∽△DBC;(2)、求线段AE的长.四、解答题(第21题12分,第22题12分,共24分)
-
21.
某中学对本校500名毕业生中考体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理、绘制成如下不完整的统计图(图①、图②),请根据统计图提供的信息,回答下列问题:
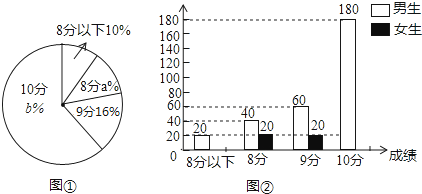 (1)、该校毕业生中男生有人,女生有人;(2)、扇形统计图中a= , b=;(3)、补全条形统计图(不必写出计算过程);(4)、若本校500名毕业生中随机抽取一名学生,这名学生该项测试成绩在8分以下的概率是多少?22.
(1)、该校毕业生中男生有人,女生有人;(2)、扇形统计图中a= , b=;(3)、补全条形统计图(不必写出计算过程);(4)、若本校500名毕业生中随机抽取一名学生,这名学生该项测试成绩在8分以下的概率是多少?22.如图,⊙O的直径AB的长为10,直线EF经过点B且∠CBF=∠CDB.连接AD.
 (1)、求证:直线EF是⊙O的切线;(2)、若点C是弧AB的中点,sin∠DAB= ,求△CBD的面积.
(1)、求证:直线EF是⊙O的切线;(2)、若点C是弧AB的中点,sin∠DAB= ,求△CBD的面积.五、解答题(满分12分)
-
23. 为奖励在文艺汇演中表现突出的同学,班主任派生活委员小亮到文具店为获奖同学购买奖品.小亮发现,如果买1个笔记本和3支钢笔,则需要18元;如果买2个笔记本和5支钢笔,则需要31元.(1)、求购买每个笔记本和每支钢笔各多少元?(2)、班主任给小亮的班费是100元,需要奖励的同学是24名(每人奖励一件奖品),若购买的钢笔数不少于笔记本数,求小亮有哪几种购买方案?
六、解答题(满分12分)
-
24.
周末,王爷爷骑自行车随“夕阳红自行车队”到“象牙山”游玩.早上从市区出发,1小时50分钟后,到达“象牙山”,3小时后王爷爷的儿子小王打电话告诉王爷爷去接他,同时,小王驾车从市区同一地点出发沿相同路线去接王爷爷.王爷爷在接到电话10分钟后,随自行车队一起沿原路按原速返回.如图,是“自行车队”离市区的距离y(千米)和所用时间x(时)的函数图象及小王驾车出发到接到王爷爷时离市区的距离y(千米)和所用时间x(时)的函数图象,其解析式为yEC=60x﹣290.
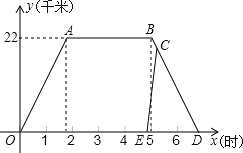 (1)、王爷爷骑车的速度是千米∕时,点D的坐标为;(2)、求小王接到王爷爷时距“象牙山”有多远?
(1)、王爷爷骑车的速度是千米∕时,点D的坐标为;(2)、求小王接到王爷爷时距“象牙山”有多远?七、解答题(满分26分)
-
25.
已知△ABC是等边三角形.
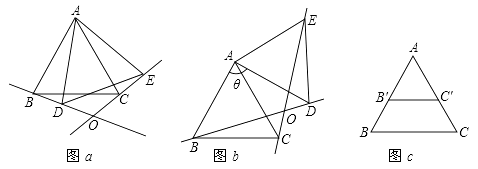 (1)、将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)、将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.①如图a,当θ=20°时,△ABD与△ACE是否全等?(填“是”或“否”),∠BOE=度;
(2)、如图c,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
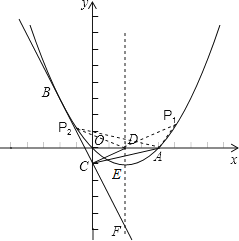
26.如图,已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D.直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
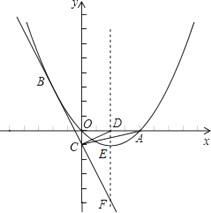 (1)、求m的值及该抛物线对应的解析式;(2)、P(x,y)是抛物线上的一点,若S△ADP=S△ADC , 求出所有符合条件的点P的坐标;(3)、
(1)、求m的值及该抛物线对应的解析式;(2)、P(x,y)是抛物线上的一点,若S△ADP=S△ADC , 求出所有符合条件的点P的坐标;(3)、点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不能,请说明理由.
-
-