2012年辽宁省锦州市中考数学试卷
试卷更新日期:2016-05-13 类型:中考真卷
一、选择题(共8小题,每小题3分,满分24分)
-
1. |﹣3|的倒数是( )A、3 B、 C、﹣3 D、﹣2. 下列各图,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、a2+a5=a7 B、(﹣ab)3=﹣ab3 C、a8÷a2=a4 D、2a2•a=2a34. 某中学礼仪队女队员的身高如下表:
3. 下列运算正确的是( )A、a2+a5=a7 B、(﹣ab)3=﹣ab3 C、a8÷a2=a4 D、2a2•a=2a34. 某中学礼仪队女队员的身高如下表:身高(cm)
165
168
170
171
172
人数(名)
4
6
5
3
2
则这个礼仪队20名女队员身高的众数和中位数分别是( )
A、168cm,169cm B、168cm,168cm C、172cm,169cm D、169cm,169cm5.如图,在△ABC中,AB=AC,AB+BC=8.将△ABC折叠,使得点A落在点B处,折痕DF分别与AB、AC交于点D、F,连接BF,则△BCF的周长是( )
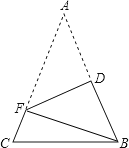 A、8 B、16 C、4 D、106. 下列说法正确的是( )A、同位角相等 B、梯形对角线相等 C、等腰三角形两腰上的高相等 D、对角线相等且垂直的四边形是正方形7. 如图,反比例函数y= (k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是( )
A、8 B、16 C、4 D、106. 下列说法正确的是( )A、同位角相等 B、梯形对角线相等 C、等腰三角形两腰上的高相等 D、对角线相等且垂直的四边形是正方形7. 如图,反比例函数y= (k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是( )
A、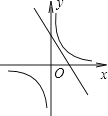 B、
B、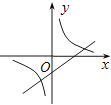 C、
C、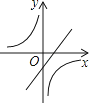 D、
D、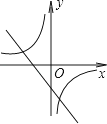 8.
8.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB'C',若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
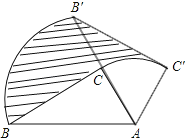 A、π B、π C、2π D、4π
A、π B、π C、2π D、4π二、填空题(每小题3分,共24分)
-
9. 计算:( +1)0﹣2﹣1+ ﹣6sin60°= .10. 函数y= 中,自变量x的取值范围是 .11. 万里长城和京杭大运河都是我国古代文明的伟大成就,其中纵贯南北的京杭大运河修建时长度大约为1 790 000米,是非常杰出的水利工程.将数据1 790 000米用科学记数法表示为米.12. 不等式组 的解集是 .13. 已知三角形的两条边长分别是7和3,第三边长为整数,则这个三角形的周长是偶数的概率是 .14. 某品牌自行车进价为每辆800元,标价为每辆1200元.店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润率不低于5%,则最多可打折.15.
如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是cm.
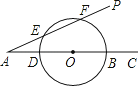 16.
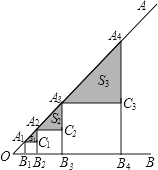
16.如图,正方形A1B1B2C1 , A2B2B3C2 , A3B3B4C3 , …,AnBnBn+1Cn , 按如图所示放置,使点A1、A2、A3、A4、…、An在射线OA上,点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1 , S2 , S3 , …,Sn , 则Sn= .
三、解答题(每小题8分,共16分)
-
17. 先化简,再求值: ,其中x= .18.
如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
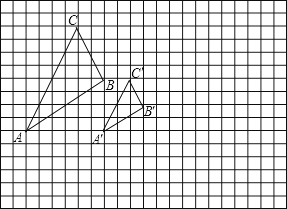 (1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
(1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.四、解答题(每小题10分,共20分)
-
19.
随着人们生活水平的提高,城市家庭私家车的拥有量越来越多.私家车给人们的生活带来很多方便,同时也给城市的道路交通带来了很大的压力,尤其是节假日期间交通拥堵现象非常严重.为了缓解交通堵塞,尽量保持道路通畅,某市有关部门号召市民“在节假日期间选择公共交通工具出行”.为了了解市民的意见和态度,有关部门随机抽取了若干市民进行了调查.经过统计、整理,制作统计图如图.请回答下列问题:
 (1)、这次抽查的市民总人数是多少?(2)、分别求出持“赞成”态度、“无所谓”态度的市民人数以及持“无所谓”态度的人数占总人数的百分比,并补全条形统计图和扇形统计图;(3)、若该市约有18万人,请估计对这一问题持“赞成”态度的人数约是多少?20. 某部队要进行一次急行军训练,路程为32km.大部队先行,出发1小时后,由特种兵组成的突击小队才出发,结果比大部队提前20分钟到达目的地.已知突击小队的行进速度是大部队的1.5倍.(1)、求大部队的行进速度.(列方程解应用题)
(1)、这次抽查的市民总人数是多少?(2)、分别求出持“赞成”态度、“无所谓”态度的市民人数以及持“无所谓”态度的人数占总人数的百分比,并补全条形统计图和扇形统计图;(3)、若该市约有18万人,请估计对这一问题持“赞成”态度的人数约是多少?20. 某部队要进行一次急行军训练,路程为32km.大部队先行,出发1小时后,由特种兵组成的突击小队才出发,结果比大部队提前20分钟到达目的地.已知突击小队的行进速度是大部队的1.5倍.(1)、求大部队的行进速度.(列方程解应用题)五、解答题(每小题10分,共20分)
-
21.
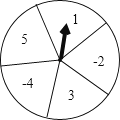
如图,有一个可以自由转动的转盘被平均分成五个扇形,五个扇形内部分别标有数字.﹣2、3、﹣4、5.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为m,n(当指针指在边界线时视为无效,重转),从而确定一个点的坐标为A(m,n).请用列表或者画树状图的方法求出所有可能得到的点A的坐标,并求出点A在第一象限内的概率.
 22.
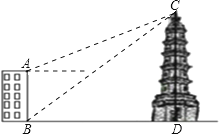
22.如图,大楼AB高16米,远处有一塔CD,某人在楼底B处测得塔顶的仰角为38.5°,爬到楼顶A处测得塔顶的仰角为22°,求塔高CD及大楼与塔之间的距离BD的长.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )
六、解答题(每小题10分,共20分)
-
23.
如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作直线DE垂直BC于F,且交BA的延长线于点E.
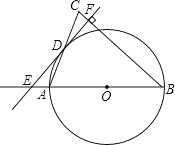 (1)、求证:直线DE是⊙O的切线;(2)、若cos∠BAC= ,⊙O的半径为6,求线段CD的长.24. 某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.(1)、求y与x的函数关系式并直接写出自变量x的取值范围.(2)、每件玩具的售价定为多少元时,月销售利润恰为2520元?(3)、每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
(1)、求证:直线DE是⊙O的切线;(2)、若cos∠BAC= ,⊙O的半径为6,求线段CD的长.24. 某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.(1)、求y与x的函数关系式并直接写出自变量x的取值范围.(2)、每件玩具的售价定为多少元时,月销售利润恰为2520元?(3)、每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?七、解答题(本题12分)
-
25.
已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
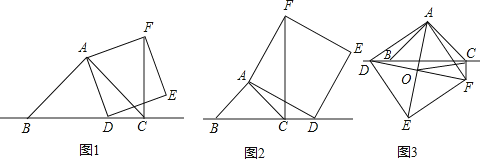 (1)、如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.(2)、如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;(3)、如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
(1)、如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.(2)、如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;(3)、如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.八、解答题(本题14分)
-
26.
如图,抛物线y=ax2+bx﹣3交y轴于点C,直线l为抛物线的对称轴,点P在第三象限且为抛物线的顶点.P到x轴的距离为 ,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B.
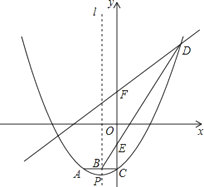 (1)、求抛物线的表达式;(2)、直线y= x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y= x+m的表达式;(3)、若N为平面直角坐标系内的点,在直线y= x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、直线y= x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y= x+m的表达式;(3)、若N为平面直角坐标系内的点,在直线y= x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
-