2020年暑期衔接训练人教版数学八年级下册:第4讲 平行四边形
试卷更新日期:2020-07-17 类型:复习试卷
一、单选题
-
1. 在下列性质中,平行四边形不一定具有的是( )A、对边相等 B、对角互补 C、对边平行 D、对角相等2. 平行四边形的一个内角是70°,则其他三个角是( )A、70°,130°,130° B、110°,70°,120° C、110°,70°,110° D、70°,120°,120°3. 如右图要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为( )
 A、30 m B、70 m C、105m D、140m4. 如图,▱ABCD的对角线AC、BD相交于点O , 且AC+BD=24.若△OAB的周长是20,则AB的长为( )
A、30 m B、70 m C、105m D、140m4. 如图,▱ABCD的对角线AC、BD相交于点O , 且AC+BD=24.若△OAB的周长是20,则AB的长为( )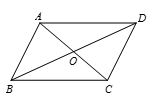 A、8 B、9 C、10 D、125. 下面给出的四边形ABCD中,∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的条件是( )A、3∶4∶3∶4 B、3∶3∶4∶4 C、2∶3∶4∶5 D、3∶4∶4∶36. 如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时, 那么下列结论成立的是( ).
A、8 B、9 C、10 D、125. 下面给出的四边形ABCD中,∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的条件是( )A、3∶4∶3∶4 B、3∶3∶4∶4 C、2∶3∶4∶5 D、3∶4∶4∶36. 如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时, 那么下列结论成立的是( ). A、线段EF的长逐渐增大 B、线段EF的长逐渐减少 C、线段EF的长不变 D、线段EF的长不能确定7. 如图,下面不能判定四边形ABCD是平行四边形的是( )
A、线段EF的长逐渐增大 B、线段EF的长逐渐减少 C、线段EF的长不变 D、线段EF的长不能确定7. 如图,下面不能判定四边形ABCD是平行四边形的是( ) A、 B、 C、 D、8. 如图,在▱ABCD中,P是对角线BD上的一点,过点作EF∥AB,与AD和BC分别交于点E和点F,连结AP,CP。已知AE=4,EP=2,∠ABC=60°则阴影部分的面积是( )
A、 B、 C、 D、8. 如图,在▱ABCD中,P是对角线BD上的一点,过点作EF∥AB,与AD和BC分别交于点E和点F,连结AP,CP。已知AE=4,EP=2,∠ABC=60°则阴影部分的面积是( ) A、 B、 C、 D、89. 如图,正方形ABCD和▱AEFC,点B在EF边上,若正方形ABCD和▱AEFC的面积分别是S1、S2的大小关系是( )
A、 B、 C、 D、89. 如图,正方形ABCD和▱AEFC,点B在EF边上,若正方形ABCD和▱AEFC的面积分别是S1、S2的大小关系是( ) A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定10. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB于E,在线段
A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定10. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB于E,在线段AB上,连接EF、CF.则下列结论:①∠BCD=2∠DCF;②∠ECF=∠CEF;③S△BEC=2S△CEF;④∠DFE=3∠AEF,其中一定正确的是( )
 A、②④ B、①②④ C、①②③④ D、②③④
A、②④ B、①②④ C、①②③④ D、②③④二、填空题
-
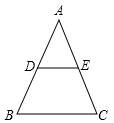
11. 在平行四边形ABCD中,若 与 的度数之比为 ,则 的度数为 .12. 如图所示,DE是△ABC的中位线,BC=8,则DE= .
 13. 平行四边形ABCD的周长是30,AC,BD相交于点0, 的周长比 的周长大3,则AB=.14. 在四边形ABCD中,对角线AC ⊥BD且AC=4,BD=8,E、F分别是边AB.CD的中点,则EF= .
13. 平行四边形ABCD的周长是30,AC,BD相交于点0, 的周长比 的周长大3,则AB=.14. 在四边形ABCD中,对角线AC ⊥BD且AC=4,BD=8,E、F分别是边AB.CD的中点,则EF= .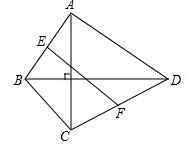 15. 如图,在四边形 中, ,点 分别从点 同时出发,点 以 的速度由点 向点 运动,点 以 的速度由点 向点 运动设运动时间为 .当 .时, 为平行四边形的一边.
15. 如图,在四边形 中, ,点 分别从点 同时出发,点 以 的速度由点 向点 运动,点 以 的速度由点 向点 运动设运动时间为 .当 .时, 为平行四边形的一边.
三、解答题
-
16. 如图,点 , 是四边形 的对角线 上的两点,且 , , .求证: .
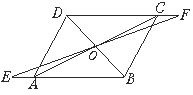
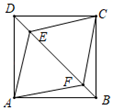 17. 如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF . 求证:四边形DEBF是平行四边形.
17. 如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF . 求证:四边形DEBF是平行四边形.