2020年暑期衔接训练人教版数学八年级下册：第2讲 勾股定理
试卷更新日期：2020-07-17 类型：复习试卷
一、单选题
-
1. 如图，两个正方形的面积分别是100和36，则字母B所代表的正方形的面积是（ ）
A、8 B、10 C、64 D、1362. 如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，则AB的长为（ ）
A、5 B、25 C、6 D、3. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为 ，则正方形A，B，C，D的面积之和为( )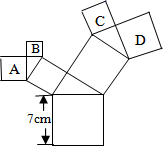
A、 B、 C、 D、4. 如图，Rt△ABC中，∠ACB=90°，若AB=15，则正方形ADEC和正方形BCFG的面积之和为（ ）
A、150 B、200 C、225 D、无法计算5. 下列说法正确的是（ ）A、若 a、b、c是△ABC的三边，则a2＋b2＝c2 B、若 a、b、c是Rt△ABC的三边，则a2＋b2＝c2 C、若 a、b、c是Rt△ABC的三边， ，则a2＋b2＝c2 D、若 a、b、c是Rt△ABC的三边， ，则a2＋b2＝c26. 边长为5的菱形ABCD按如图所示放置在数轴上， 其中A点表示数-2，C点表示数6，则BD=（ ）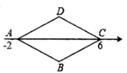
A、4 B、6 C、8 D、107. 如图，Rt△ABC中，∠ACB＝90°，以AC，BC为直径作半圆S1和S2 ， 且S1+S2＝2π，则AB的长为（ ）
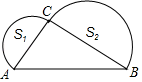A、16 B、8 C、4 D、28. 如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分以的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）
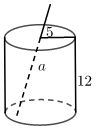A、12≤a≤13 B、12≤a≤15 C、5≤a≤12 D、5≤a≤l39. 已知Rt△ABC中，∠C=90°，若a+b=10cm，c=8cm，则Rt△ABC的面积为（ ）A、9cm2 B、18cm2 C、24cm² D、36cm210. 如图，正方形ABCD的边长为2，其面积标记为S1 ， 以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2 ， …，按照此规律继续下去，则S9的值为（ ）
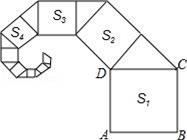A、（ ）6 B、（ ）7 C、（ ）6 D、（ ）7二、填空题
-
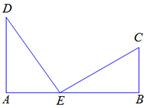
11. 直角三角形两直角边长分别为2 ＋1，2 －1，则它的斜边长为 ．12. 生活经验表明：靠墙摆放梯子时，若梯子底端离墙约为梯子长度的 时，则梯子比较稳定．现有一长度为9 m的梯子，当梯子稳定摆放时，它的顶端能到达8.5 m高的墙头吗？(填“能”或“不能”)．13. 如图由于台风的影响，一棵树在离地面3m处折断，树顶落在离树干底部4m处，则这棵树在折断前（不包括树根）长度是.
14. 若一个直角三角形的三边分别为x，4，5，则x= 。15. 如图，在四边形ABCD中，AB＝BC＝2 ，AD＝2，∠B＝∠D＝90°，则CD=
16. 如图，OP=1，过P作PP1⊥OP ， 得OP1= ；再过P1作P1P2⊥OP1且P1P2=1，得OP2= ；又过P2作P2P3⊥OP2且P2P3=1，得OP3=2；…依此法继续作下去，得OP2019= ．
三、解答题
-
17. 如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米，那么点B将向左滑动多少米？
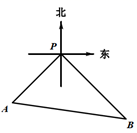
18. 如图，港口 位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一个固定方向航行，甲船沿西南方向以每小时12海里的速度航行，乙船沿东南方向以每小时16海里的速度航行，它们离开港口5小时后分别位于 、 两处，求此时 之间的距离.
