浙江省台州市仙居县2020年数学中考模拟试卷
试卷更新日期:2020-07-17 类型:中考模拟
一、选择题(题中所给的答案有且只有一个正确;本大题共10小题,每小题4分,满分40分)
-
1. -2+4=( )A、2 B、-2 C、 D、2. 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
 A、
A、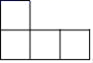 B、.
B、.  C、.
C、. 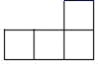 D、.
D、. 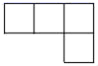 3. 下列四个图案中,是轴对称图形的是( )A、
3. 下列四个图案中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列调查方式,你认为最合适的是( )。A、要调查一批灯管的使用寿命,采全面调查的方式 B、杭州机场对旅客进行登机前安检,采用抽样调查方式 C、为了调查2019年度浙江省人均收入情况,调查省会城市杭州的人均收入 D、为了解台州市市民疫情期间的物资采购情况,采取抽样调查方式5. 如图,四边形ABCD是⊙O的内接四边形,若∠BCD=143°,则∠BOD的度数是( )。
4. 下列调查方式,你认为最合适的是( )。A、要调查一批灯管的使用寿命,采全面调查的方式 B、杭州机场对旅客进行登机前安检,采用抽样调查方式 C、为了调查2019年度浙江省人均收入情况,调查省会城市杭州的人均收入 D、为了解台州市市民疫情期间的物资采购情况,采取抽样调查方式5. 如图,四边形ABCD是⊙O的内接四边形,若∠BCD=143°,则∠BOD的度数是( )。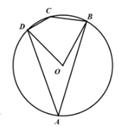 A、77 B、74° C、37° D、436. 如图,以△ABD的顶点B为圆心, 以BD为半径作弧交边AD于点E, 分别以点D、点E为圆心,BD长为半径作弧,两弧相交于不同于点B的另一点F,再过点B和点F作直线BF,则作出的直线是( )
A、77 B、74° C、37° D、436. 如图,以△ABD的顶点B为圆心, 以BD为半径作弧交边AD于点E, 分别以点D、点E为圆心,BD长为半径作弧,两弧相交于不同于点B的另一点F,再过点B和点F作直线BF,则作出的直线是( ) A、线段AD的垂线但不一定平分线段AD B、线段AD的垂直平分线 C、∠ABD的平分线 D、△ABD的中线7. 如果a>b,c<0,那么下列不等式成立的是( )。A、c-a>c-b B、a+c>b+c C、ac>bc D、8. 已知函数y=- 的图象上有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),且x1<x2<0<x3;则y1 , y2 , y3的大小关系为( )。A、y1<y2<y3 B、y3<y1<y2 C、y2<y1<y3 D、y2<y3<y19. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系,每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元,要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加x株花苗,下面列出的方程中符合题意的是( )。A、(x+3)(5-0.5x)=20 B、(x-3)(5+0.5x)=20 C、(x-3)(5-0.5x)=20 D、(x+3)(5+0.5x)=2010. 有这样一种算法,对于输入的任意一个实数,都进行“先乘以 ,再加3”的运算。现在输入一个x=4,通过第1次运算的结果为x1 , 再把x1输入进行第2次同样的运算,得到的运算结果为x2 , …,一直这样运算下去,当运算次数不断增加时,运算结果xn( )A、越来越接近4 B、越来越接近于-2 C、越来越接近2 D、不会越来越接近于一个固定的数
A、线段AD的垂线但不一定平分线段AD B、线段AD的垂直平分线 C、∠ABD的平分线 D、△ABD的中线7. 如果a>b,c<0,那么下列不等式成立的是( )。A、c-a>c-b B、a+c>b+c C、ac>bc D、8. 已知函数y=- 的图象上有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),且x1<x2<0<x3;则y1 , y2 , y3的大小关系为( )。A、y1<y2<y3 B、y3<y1<y2 C、y2<y1<y3 D、y2<y3<y19. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系,每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元,要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加x株花苗,下面列出的方程中符合题意的是( )。A、(x+3)(5-0.5x)=20 B、(x-3)(5+0.5x)=20 C、(x-3)(5-0.5x)=20 D、(x+3)(5+0.5x)=2010. 有这样一种算法,对于输入的任意一个实数,都进行“先乘以 ,再加3”的运算。现在输入一个x=4,通过第1次运算的结果为x1 , 再把x1输入进行第2次同样的运算,得到的运算结果为x2 , …,一直这样运算下去,当运算次数不断增加时,运算结果xn( )A、越来越接近4 B、越来越接近于-2 C、越来越接近2 D、不会越来越接近于一个固定的数二、填空题(本大题共6小题,每小题5分,共30分)
-
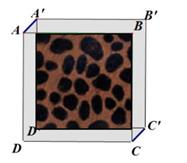
11. 因式分解:a2-4=。12. 小明化简分式如下: =(x+1)(x-1)-x²=x²-1-x²=-1,他的化简对还是错?(填写“对”或“错”) , 正确的化简结果是。13. 不等式组 的解集是。14. 有两个检查组,分别对“垃圾分类”和“违规停车”的情况进行抽查,两个检查组各随机抽取辖区内某三个小区中的一个进行检查,则两个检查组同时抽查到同一个小区的概率是。15. 如图正方形ABCD先向右平移1个单位长度,再向上平移1个单位长度, 得到正方形A'B'C'D',形成了中间深色的正方形及四周浅色的边框,已知正方形ABCD的面积为16,则四周浅色边框的面积是。
 16. 如图,在矩形ABCD中,AB= ,AD=3,E,F分别是边BC、AB上任意点,以线段EF为边,在EF上方作等边△EFG,取边EG的中点H,连接HC,则HC的最小值是。
16. 如图,在矩形ABCD中,AB= ,AD=3,E,F分别是边BC、AB上任意点,以线段EF为边,在EF上方作等边△EFG,取边EG的中点H,连接HC,则HC的最小值是。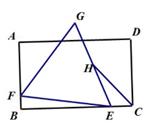
三、解答题:(本大题共8小题,17~20题每题8分,21题10分,22~23题每题12分,24题14分,共80分.)
-
17. 计算:- +(2-π)0-2sin45°18. 解方程:x(x-4)=x-4。19. 某商场计划购进A,B两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格
类型
进价(元/盏)
售价(元/盏)
A
40
55
B
60
80
(1)、若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?(2)、若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本)。20. 疫情期间,用无人机观察某段笔直街道,无人机在竖直高度为400m的C处,观测到该段街道的一端A处俯角为30°,另一端B处的俯角为45°,求该段街道AB的长。(点A,B,D在同一条直线上,结果保留根号)。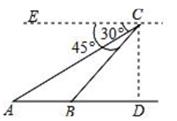 21. 甲乙两人依次测量同一圆柱体工件的横截面直径(单位:cm),测得的数据分别如表1、表2。
21. 甲乙两人依次测量同一圆柱体工件的横截面直径(单位:cm),测得的数据分别如表1、表2。表1:甲的测量数据
测量数据
9.8
9.9
10
10.1
10.3
频数
1
3
3
2
1
表2:乙的测量数据
测量数据
9.7
9.8
10
10.1
10.3
频数
1
2
3
2
2
(1)、如果在这些测量数据中选择一个数据作为工件直径的估计值,应该是那个数据?请说明理由。(2)、如果甲再测量一次,求他测量出的数据恰好是估计值的概率。(3)、请直接判断甲乙两人谁的测量技术更好(填甲或乙),你选择的统计量是 。22. 如图,在四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E。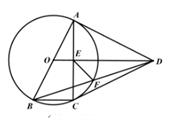 (1)、证明:AE=CE;(2)、若AC=2BC,证明:DA是⊙O的切线;(3)、在(2)条件下,连接BD交⊙O于点F,连接EF,若⊙O的直径为 ,求EF的长。23. 新型冠状肺炎给人类带来了灾难,口罩是抗击新冠肺炎的重要战略物资,国家在必要时进行价格限制,以保持价格稳定.某公司生产的口罩售价与天数的函数关系如图所示(曲线部分是以y轴为对称轴的抛物线一部分)。
(1)、证明:AE=CE;(2)、若AC=2BC,证明:DA是⊙O的切线;(3)、在(2)条件下,连接BD交⊙O于点F,连接EF,若⊙O的直径为 ,求EF的长。23. 新型冠状肺炎给人类带来了灾难,口罩是抗击新冠肺炎的重要战略物资,国家在必要时进行价格限制,以保持价格稳定.某公司生产的口罩售价与天数的函数关系如图所示(曲线部分是以y轴为对称轴的抛物线一部分)。 (1)、求口罩销售价格y(元)与天数x(天)之间的函数关系式;(2)、若这种口罩每只成本z(元)与天数x之间的关系为:
(1)、求口罩销售价格y(元)与天数x(天)之间的函数关系式;(2)、若这种口罩每只成本z(元)与天数x之间的关系为:z=
那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
24. 已知:如图1,六边形ABCDEF中,AB∥DE,BC∥EF,CD∥AF。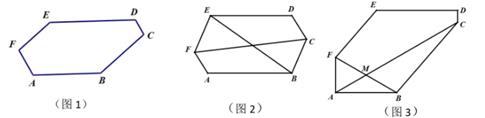 (1)、找出这个六边形中所有相等的内角 ▲ , 证明其中的一个结论。
(1)、找出这个六边形中所有相等的内角 ▲ , 证明其中的一个结论。
(2)、如果AB=DE,证明对角线BE,CF互相平分;(3)、如图,如果∠D=90°,AF= ,AB=6,DE=8,DC= ,对角线AC平分对角线BF,求MC的长。